Tema 12 Graficos
En este tema se bosquejan las posibilidades gráficas de R. En concreto vamos a describir algunas de las funciones que incluye el núcleo de R para trabajar con gráficos. Las funciones gráficas de R suelen ser genéricas y tienen un gran número de opciones. Por lo tanto, aquí nos limitaremos a comentar sus usos más comunes. Si estás interesado en conocer de manera exhaustiva el funcionamiento de alguna función consulta su ayuda.
12.1 La función plot
La función plot es una de las funciones más usadas para generar gráficos en R. Se trata de una función genérica, por lo que puede ser invocada para representar gráficamente distintos tipos de datos. La función plot es de nivel alto, es decir, genera un nuevo gráfico al ser invocada (las funciones de nivel bajo añaden información a un gráfico ya existente). En las siguientes secciones vamos a analizar algunas posibilidades de esta función.
12.1.1 Diagrama de dispersión
La función plot permite generar un diagrama de dispersión (scatter plot). Veamos un ejemplo:
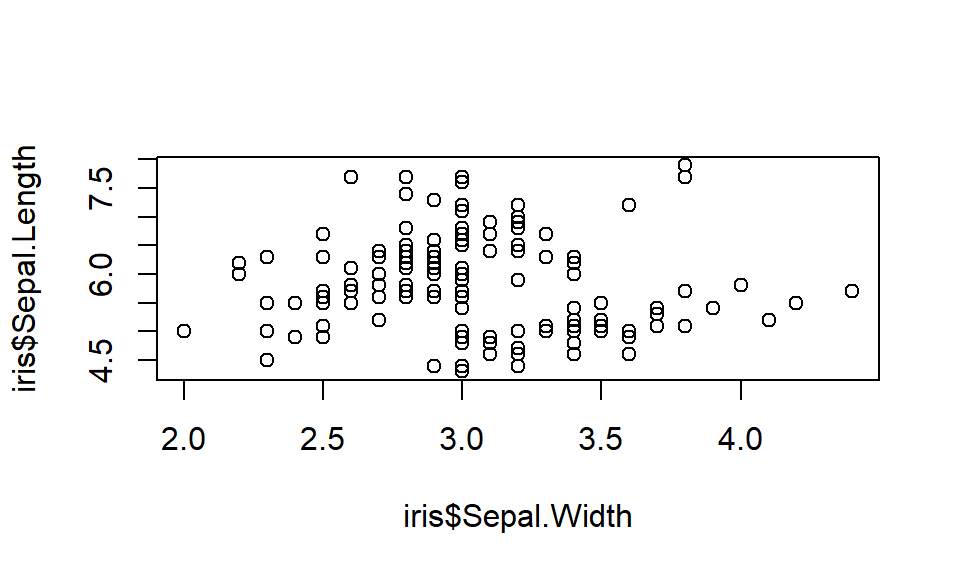
En este caso se muestra la longitud de sépalo frente a la anchura de sépalo de las flores del data frame iris. Se han usado dos vectores para especificar los datos, pero también se permite especificar los datos mediante una lista con componentes x e y o mediante una matriz con dos columnas.
Veamos otro ejemplo en el que se crean los puntos (datos) a visualizar:
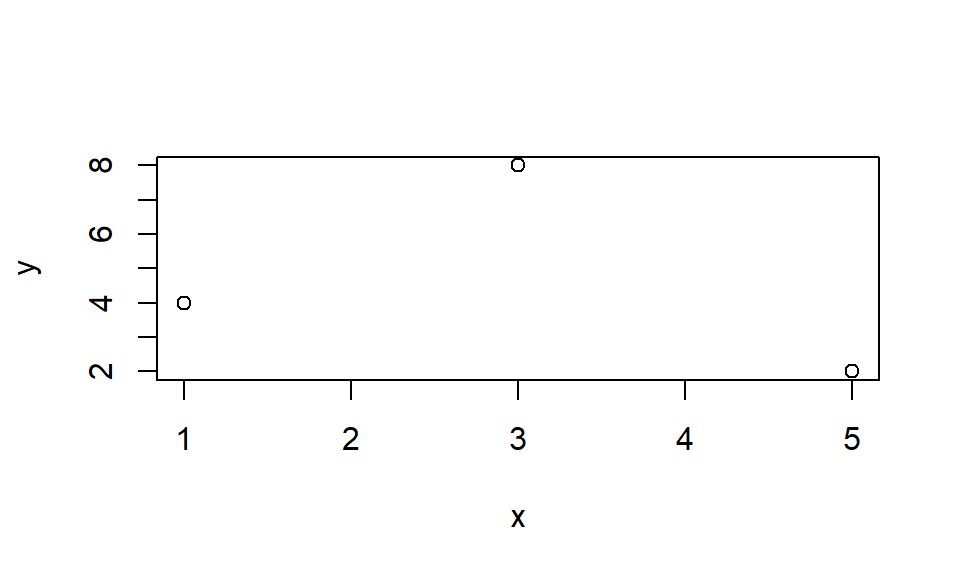
En este último ejemplo se visualizan los puntos (1,4), (5, 2) y (3, 8).
Si usamos un vector como fuente de datos, se muestra los valores del vector frente a sus índices:

12.1.2 Serie temporal
Una serie temporal es una secuencia de datos medidos en determinados momentos, generalmente equidistantes en el tiempo, y ordenados cronológicamente. plot nos permite visualizar una serie temporal:
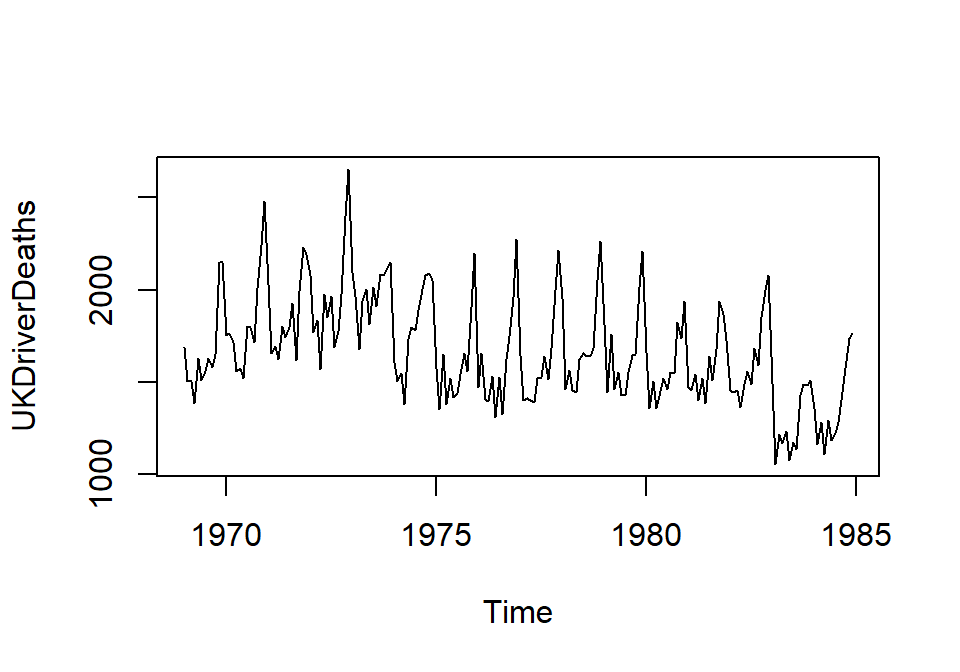
12.1.3 Visualizar una función
Podemos visualizar los valores de una función real de variable real si almacenamos en un vector una serie de valores de x (en orden creciente) y en otro vector sus correspondientes valores de y para la función. Por ejemplo, vamos a visualizar la función \(y = x^2 + 5\) para 7 valores equidistantes de x en el intervalo [-10, 10]:
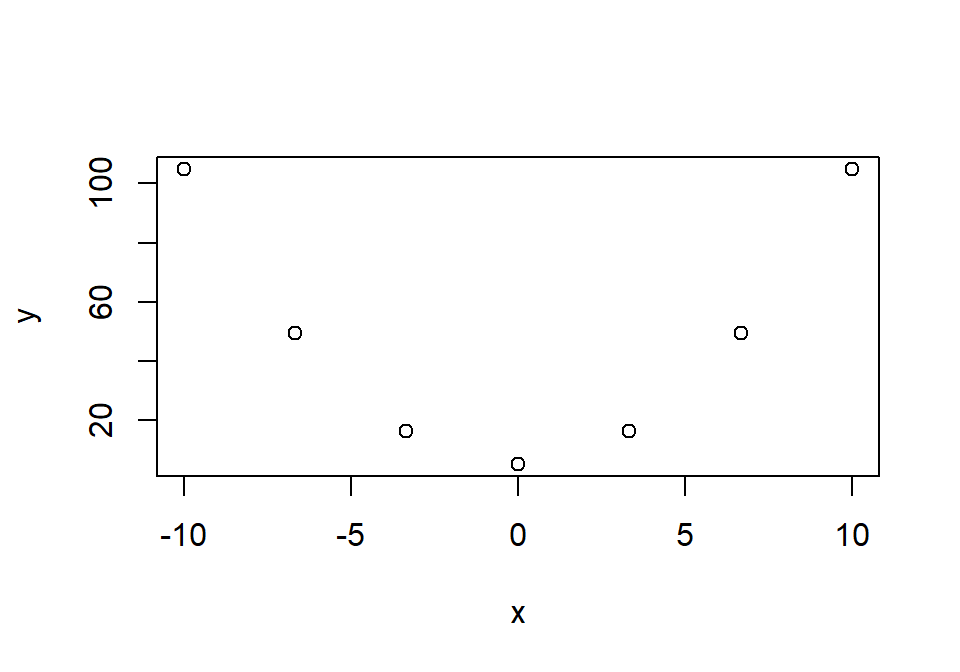
El parámetro type de plot permite visualizar los datos de distintas formas. Por defecto, este parámetro vale "p" y dibuja los puntos especificados, pero también se puede dibujar las líneas que unen los puntos, con "l", o líneas y puntos con "b" (hay más posibilidades):

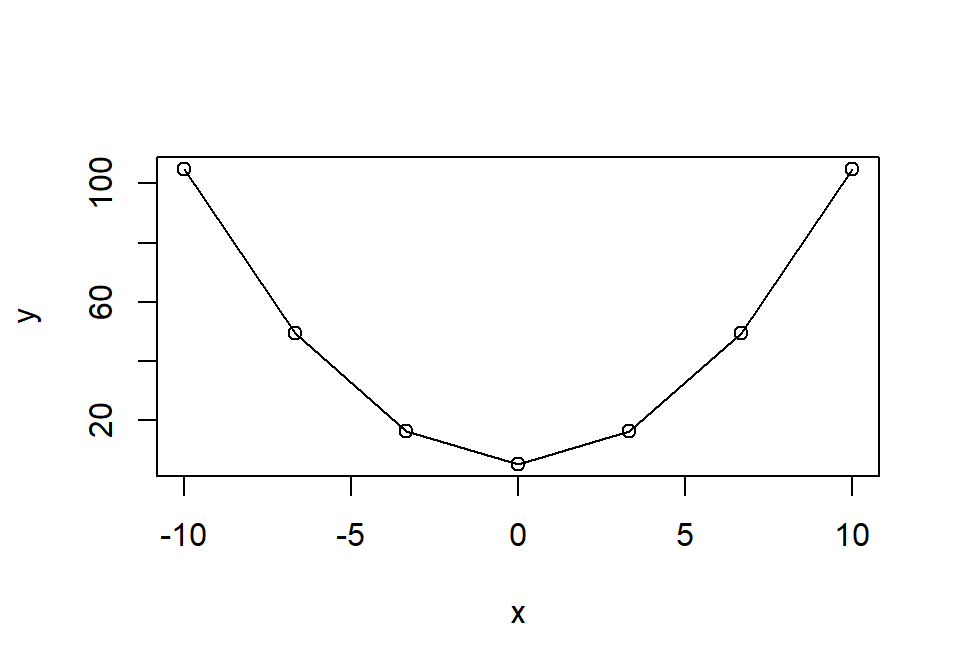
Para visualizar una función con más precisión basta con especificar más puntos de la función:
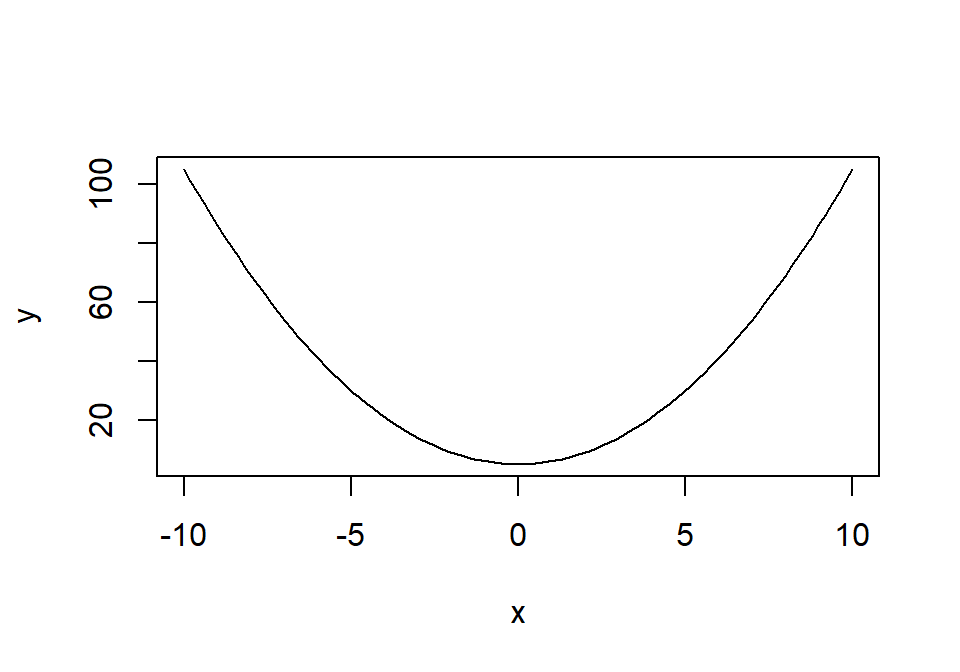
La función curve es una alternativa a plot para visualizar la curva asociada a una función. Consulta su ayuda para ver todas las posibilidades:

12.1.4 Factores y diagramas de caja
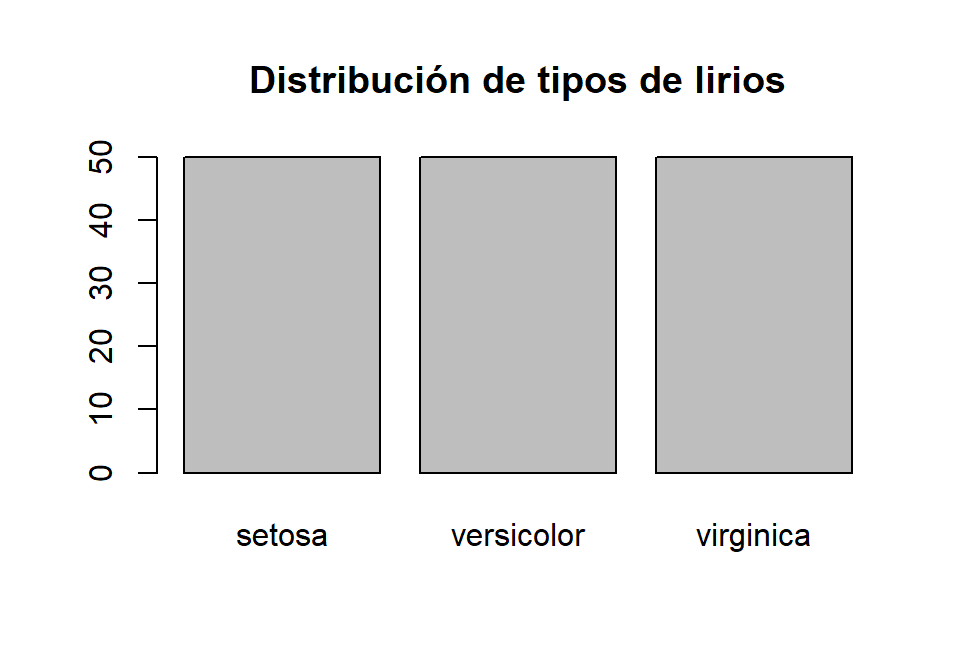
En el caso de que le pasemos a plot un factor obtendremos un diagrama de barras con las frecuencias de las distintas categorías:

Podemos observar que existen 50 datos de las tres especies de lirio del conjunto de datos iris. Podríamos obtener un resultado similar con la función barplot:
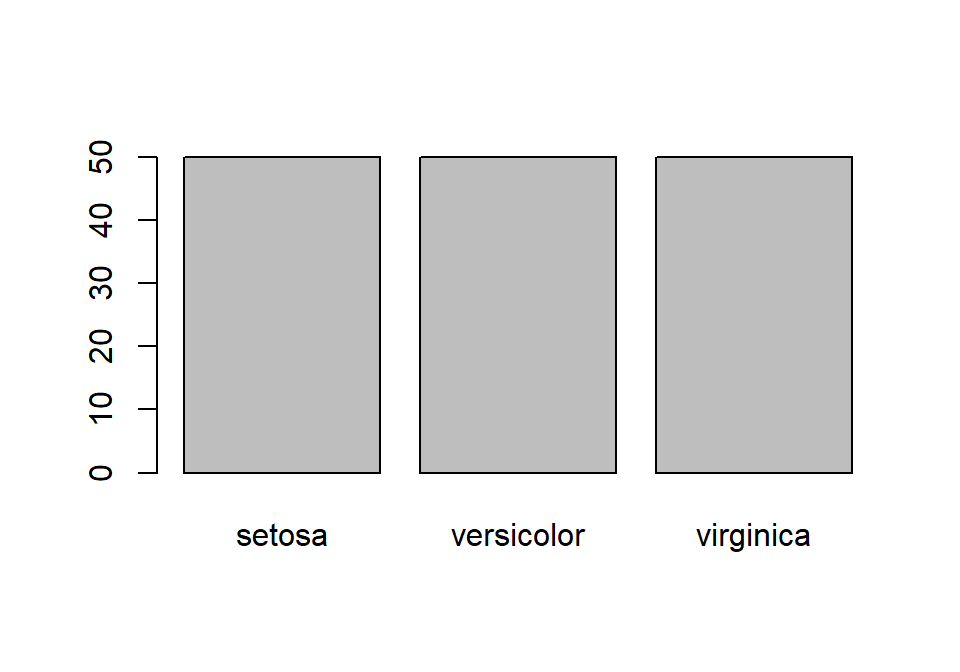
La función barplot también funciona con vectores:

Si usamos un factor y un vector numérico, se obtiene un diagrama de cajas (o de cajas y bigotes o box plot) por cada categoría del factor. Por ejemplo, veamos la distribución de la longitud de pétalo para las distintas categorías de lirios:
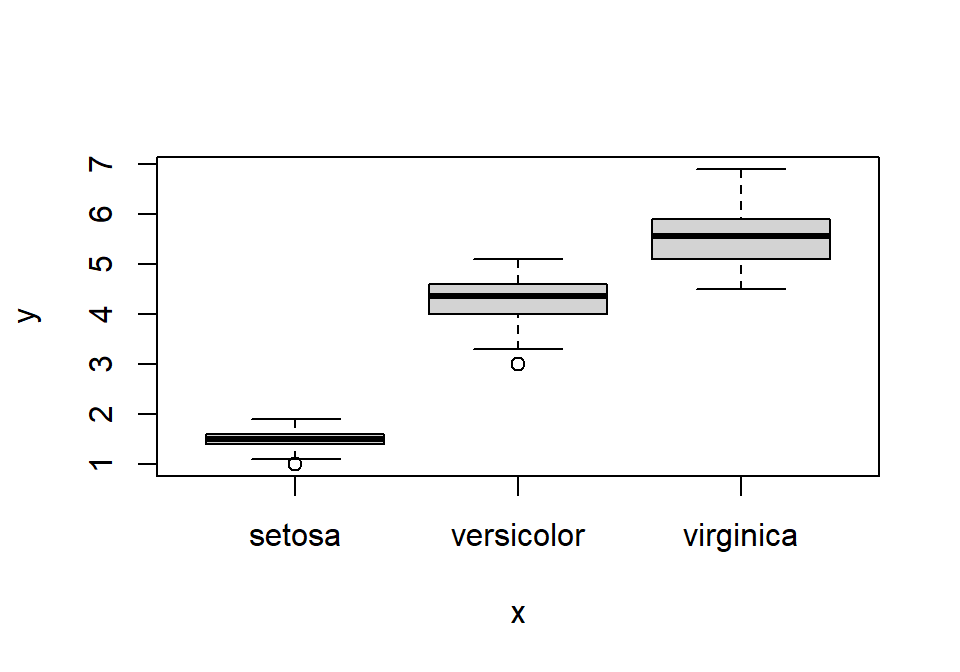
La función boxplot es una alternativa a plot para visualizar diagramas de cajas:
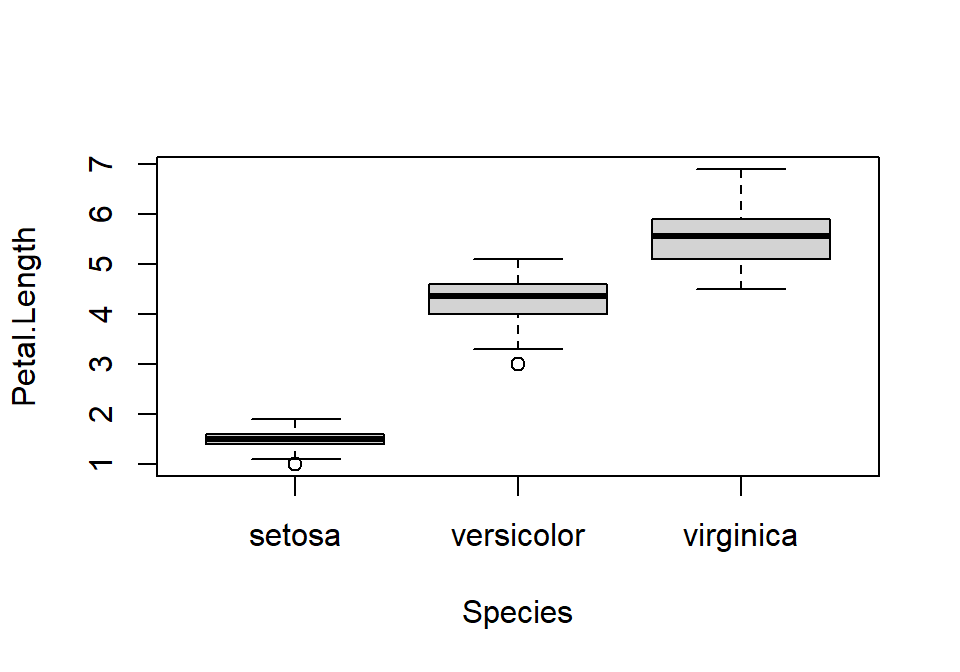
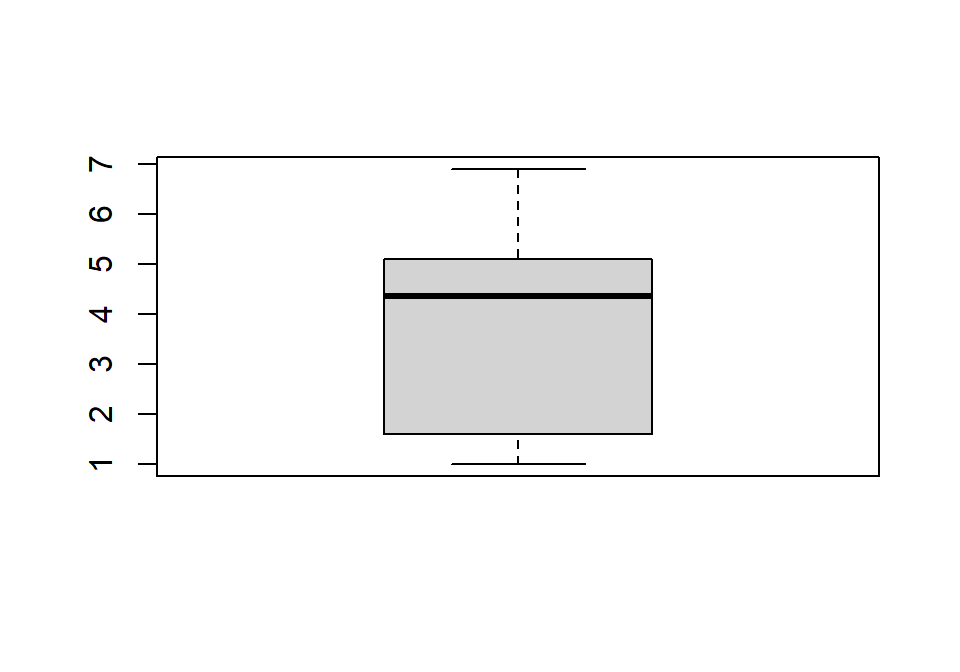
boxplot también permite generar un diagrama de cajas con los elementos de un vector. Por ejemplo, veamos el diagrama de cajas de la longitud de pétalo de todas las flores de iris:
12.1.5 Diagramas de dispersión emparejados
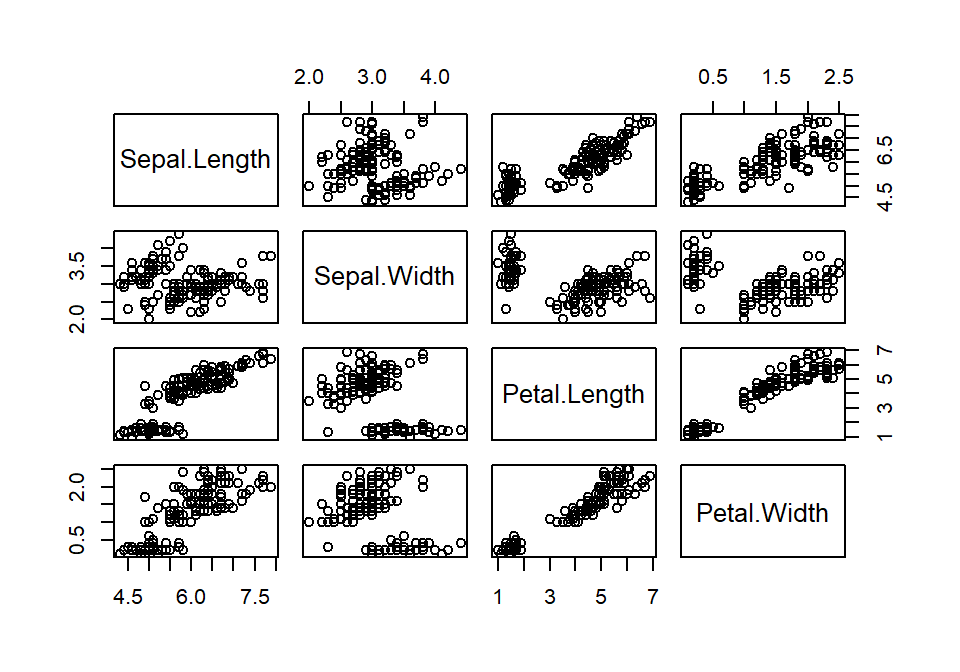
Cuando plot recibe como parámetro un data frame genera diagramas de dispersión para todos los pares de variables en el data frame:

Viendo el gráfico parece que la correlación lineal entre longitud y anchura de pétalo es alta. La función pairs es similar a este último uso de plot.
La función coplot permite generar distintos diagramas de dispersión en función de un factor:

12.2 Personalización de un gráfico
Existen muchas posibilidades para configurar el aspecto de un gráfico. En esta sección vamos a ver algunas. Observa este ejemplo:
x <- seq(0, 8*pi, by = 0.1)
plot(x, sin(x), type = "l", xlab = "x", ylab = "Seno",
main = "Función seno")
En este ejemplo se han usado textos para etiquetar los ejes del gráfico y se ha indicado un título. Es posible indicar el tipo de fuente y el color en que aparecen los textos.
Se puede especificar los límites de los ejes con los parámetros xlim e ylim y una malla de fondo con la función grid:
plot(x, sin(x), type = "l", xlab = "x", ylab = "Seno",
main = "Función seno", ylim = c(-1.5, 1.5))
grid()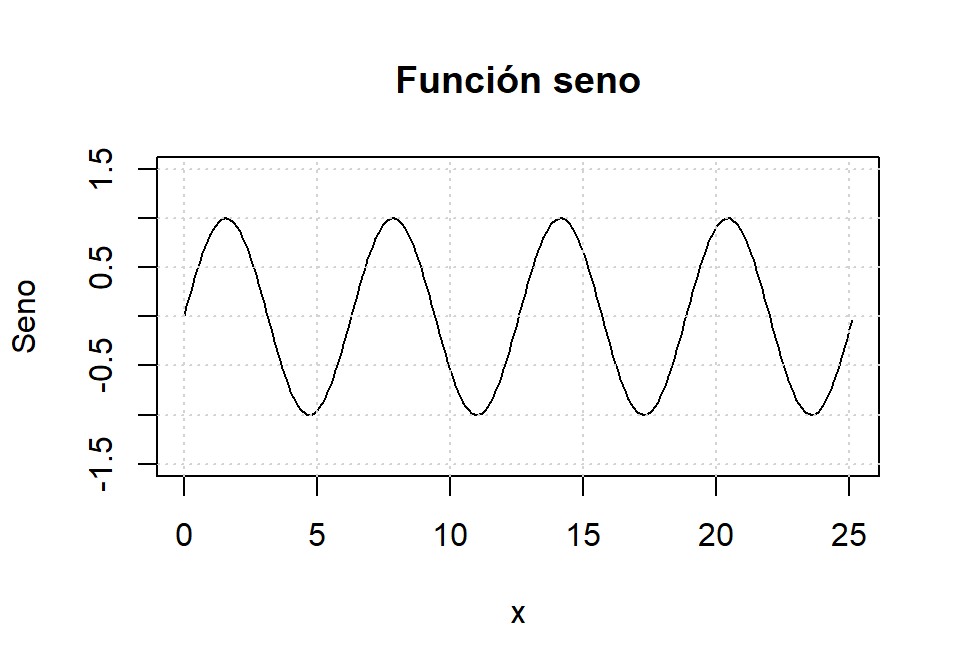
12.2.1 Tipos de línea, puntos y colores
Existen opciones para especificar los colores con los que se dibuja o los tipos de puntos y líneas. Veamos algún ejemplo:
ang <- seq(0, 2*pi, length.out = 100)
plot(cos(ang), sin(ang), type = "l", col = "red", lty = "dashed",
lwd = 3, asp = 1)
grid()
En el ejemplo se ha dibujado una circunferencia de color rojo (parámetro col), con líneas discontinuas (lty es el estilo de línea) y con una anchura de 3 unidades (parámetro lwd). El parámetro asp sirve para gestionar la proporción entre las distancias en los ejes x e y, si no se hubiera utilizado la circunferencia hubiera aparecido achatada.
Vamos a ver otro ejemplo con el estilo de los puntos:
ang <- seq(0, 2*pi, length.out = 16)
plot(cos(ang), sin(ang), col = "green", pch = 19, cex = 1.5, asp = 1)
grid()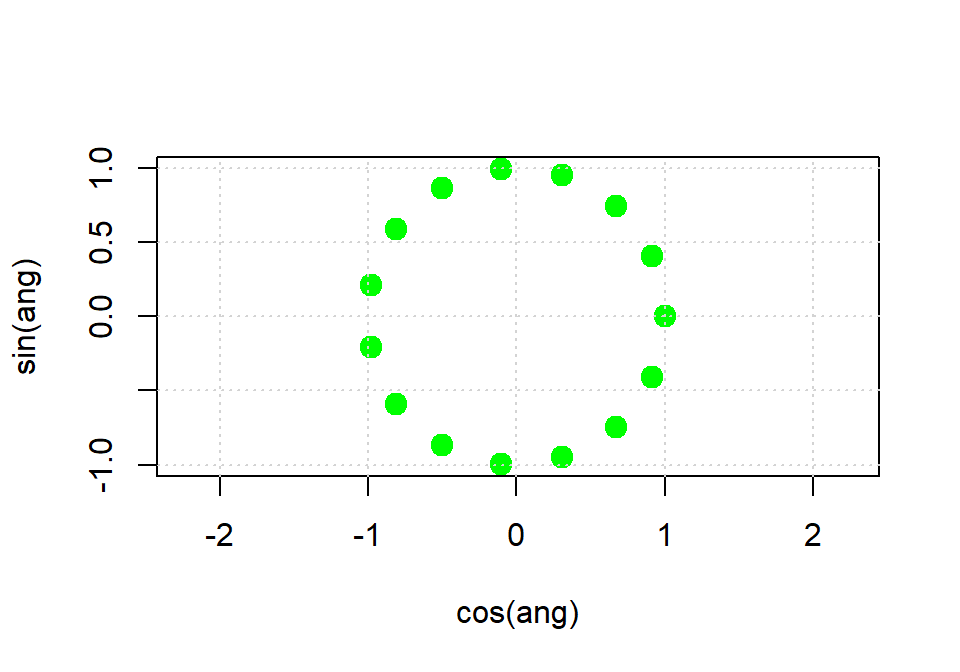
En este caso el parámetro pch indica el tipo de punto y cex su tamaño (1.5 veces el tamaño por defecto).
La función colors devuelve un vector con los colores disponibles. El siguiente gráfico muestra los distintos tipos de punto que se pueden usar con el parámetro pch.
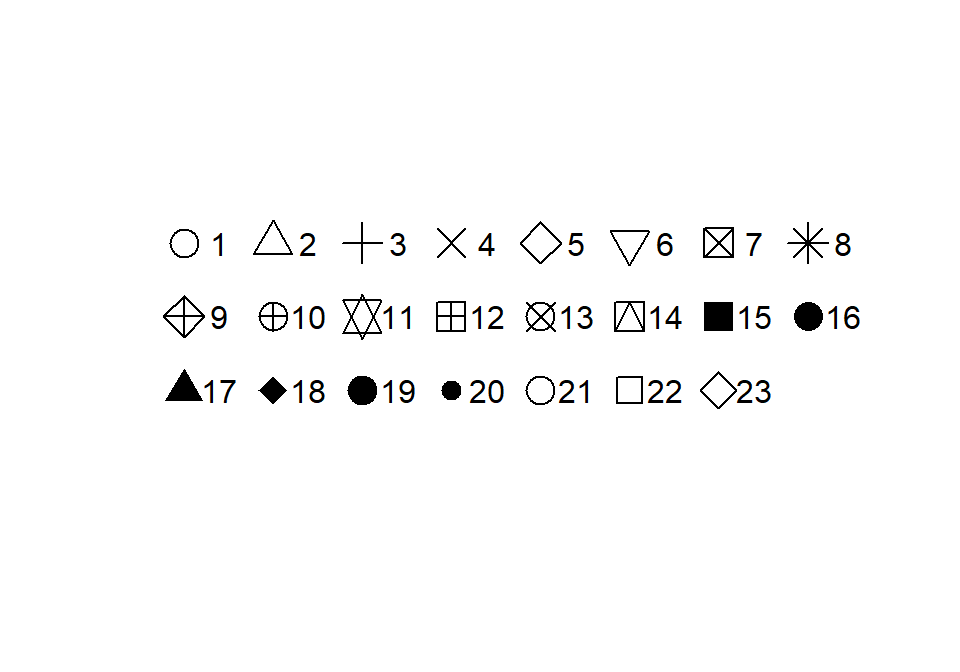
12.3 Funciones de nivel bajo
Las funciones de nivel bajo sirven para añadir información a un gráfico existente creado con una función de nivel alto, como plot. Vamos a estudiar alguna de ellas.
12.3.1 Funciones points y lines
points(x, y) y lines(x, y) añaden puntos o líneas conectadas, respectivamente, al gráfico actual. En estas funciones se puede usar el argumento type de plot, siendo su valor por defecto "p" para points y "l" para lines.
x <- seq(0, 8*pi, by = 0.1)
plot(x, sin(x), type = "l", col = "blue")
lines(x, cos(x), col = "red", lty = "dashed") # añade líneas con coseno
grid()
Veamos ahora un uso de points. Vamos a generar puntos aleatorios en el cuadrado de esquinas (-1, -1) y (1, 1) y vamos a dibujar con distinto color a los puntos a la izquierda y derecha del eje de ordenadas:
x <- runif(100, min = -1, max = 1)
y <- runif(100, min = -1, max = 1)
plot(x[x <= 0], y[x <= 0], pch = 19, col = "blue", xlim = c(-1, 1),
ylim = c(-1, 1), xlab = "x", ylab = "y", asp = 1)
points(x[x > 0], y[x > 0], pch = 19, col = "red")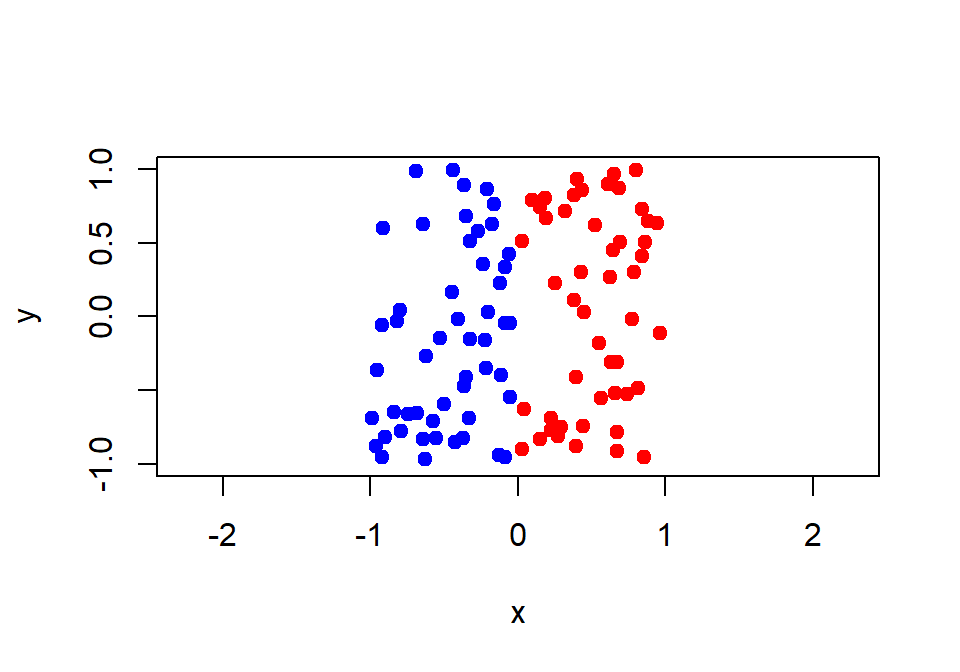
12.3.2 Función abline
La función abline sirve para añadir una línea a un gráfico. Esta función tiene varios parametros con nombre, que sirven para especificar de forma sencilla distintos tipos de líneas:
abline(a, b): línea de pendiente b y ordenada en el origen aabline(h=y): línea horizontalabline(v=x): línea vertical
Veamos un ejemplo:
# El siguiente plot crea un gráfico sin dibujar nada (type = "n")
plot(0, xlim = c(-5, 5), ylim = c(-3, 3), type = "n")
abline(1, 2, col = "red") # línea y = 2x + 1
abline(h = 2, col = "green") # línea y = 2
abline(v = 3, col = "violet") # línea x = 3
grid()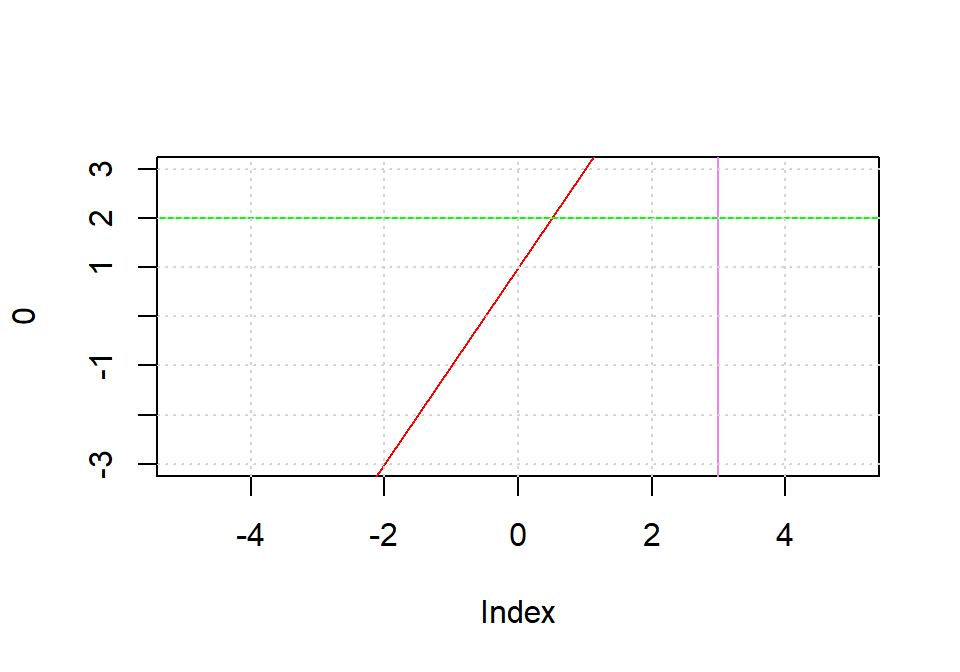
La función abline también permite dibujar la recta de regresión asociada a un modelo lineal:
plot(iris$Petal.Width, iris$Petal.Length)
modelo <- lm(Petal.Length ~ Petal.Width, data = iris)
abline(modelo, col = "red")
Como ejemplo adicional vamos a generar 20 muestras de tamaño 100 de una \(\mathcal{N}(2, 3)\) y vamos a visualizar los intervalos de confianza del 90% de la media de acuerdo a las muestras.
muestras <- matrix(rnorm(100*20, 2, 3), nrow = 20)
medias <- apply(muestras, 2, mean)
int_conf <- cbind(medias - qnorm(0.95)*3/sqrt(20),
medias + qnorm(0.95)*3/sqrt(20))
plot(c(min(int_conf), max(int_conf)), c(0, 21), type = "n",
xlab = "Intervalo de confianza 90%", ylab = "muestra")
for (m in 1:20) {
if (int_conf[m, 1] <= 2 && 2 <= int_conf[m, 2]) {
lines(c(int_conf[m, 1],int_conf[m, 2]), c(m, m), col = "blue")
} else {
lines(c(int_conf[m, 1],int_conf[m, 2]), c(m, m), col = "red")
}
}
abline(v = 2)
12.3.3 Función text
Esta función permite escribir texto en el gráfico:
# El siguiente plot crea un gráfico sin dibujar nada (type = "n")
plot(0, xlim = c(-5, 5), ylim = c(-3, 3), type = "n")
abline(h = 2, col = "green") # línea y = 2
abline(v = 3, col = "violet") # línea x = 3
grid()
text(0, 2.3, "Línea horizontal")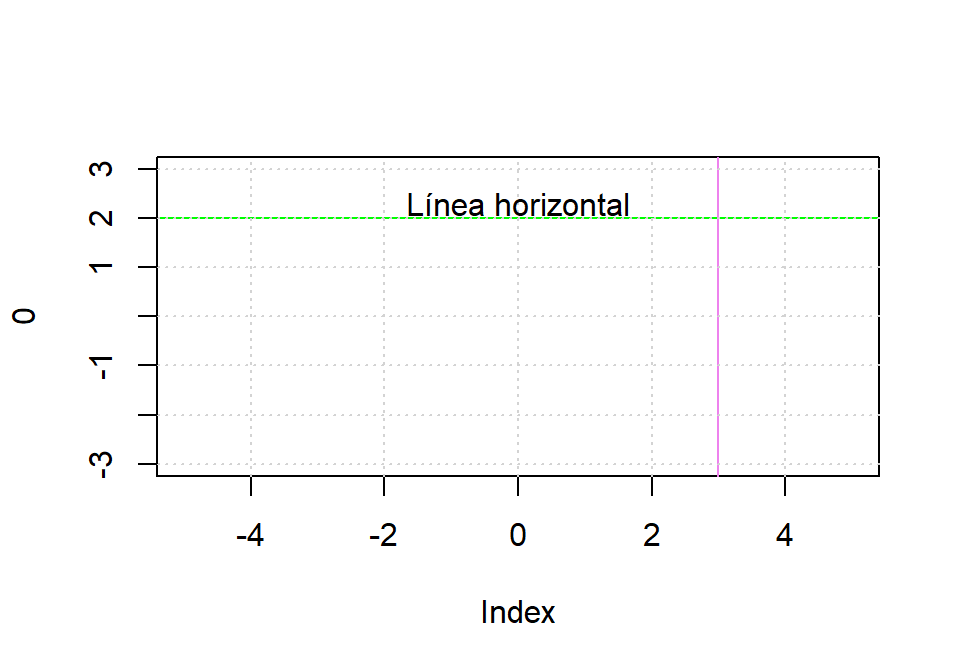
La función text tiene parámetros para especificar el tipo de letra, justificación del texto, tamaño, etcétera.
12.3.4 Función polygon
Esta función dibuja un polígono, que puede ser rellenado con color y/o líneas opcionalmente:
plot(0, xlim = c(0, 1.5), ylim = c(0, 3), type = "n")
x <- c(0, 1, 1, 0.5, 0)
y <- c(0, 0, 1, 2, 1)
polygon(x, y, col = "yellow", border = "red")
La función polygon puede utilizarse para destacar una zona de dibujo. Por ejemplo, en el siguiente gráfico se dibujan 100 puntos aletorios uniformemente distribuidos en el cuadrado de esquinas (-1, -1) y (1, 1) y se usa la función polygon para destacar el primer cuadrante:
x <- runif(100, min = -1, max = 1)
y <- runif(100, min = -1, max = 1)
plot(x, y, pch = 19, asp = 1)
x <- c(0, 1, 1, 0)
y <- c(0, 0, 1, 1)
polygon(x, y, col = rgb(1, 0, 0, 0.2), border = NA)
Observa que para especificar el color del polígono se ha usado la función rgb, que permite especificar un color como una combinación de los colores red, green, blue, con el valor de cada color especificado como un valor real en el rango [0, 1], siendo 0 que no se usa y 1 que se usa totalmente. El último parámetro de rgb, que vale 0.2 en el ejemplo, es el nivel de transparencia. También hay que especificarlo en el rango [0, 1], significando 1 totalmente opaco.
12.3.5 Función legend
La función legend añade una leyenda al gráfico actual en un determinado lugar. Vamos a ver algún ejemplo:
x <- seq(0, 8*pi, by = 0.1)
plot(x, sin(x), type = "l", col = "blue")
lines(x, cos(x), col = "red", lty = "dashed")
grid()
legend("topright", legend = c("seno", "coseno"),
col = c("blue", "red"), lty = c("solid", "dashed"))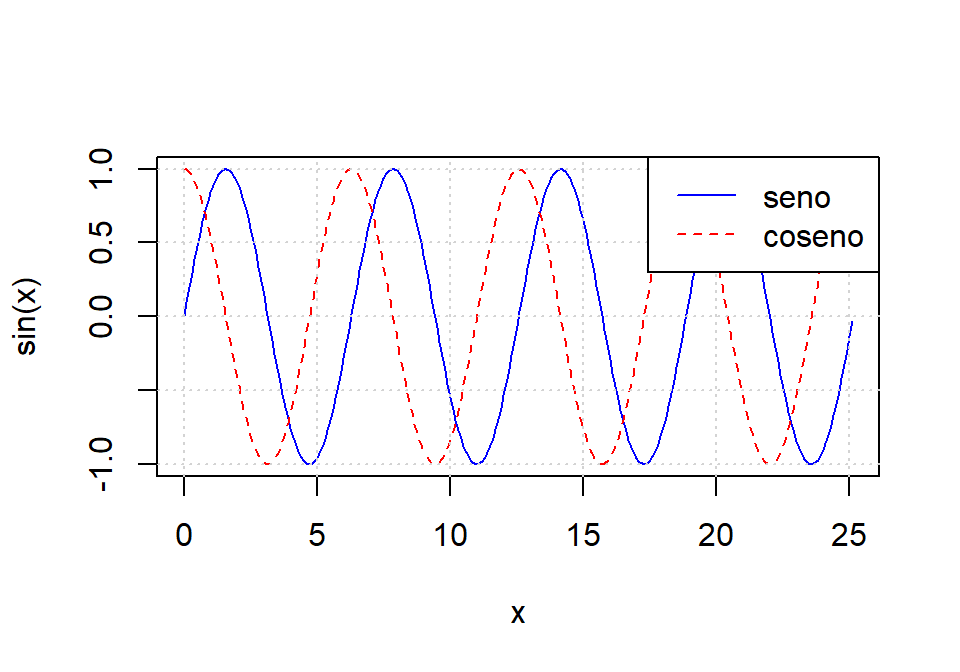
Veamos otro ejemplo con un gráfico previo:
x <- runif(100, min = -1, max = 1)
y <- runif(100, min = -1, max = 1)
plot(x[x <= 0], y[x <= 0], pch = 19, col = "blue", xlim = c(-1, 1),
ylim = c(-1, 1), asp = 1)
points(x[x > 0], y[x > 0], pch = 19, col = "red")
legend("topleft", legend = c("neg", "pos"), col = c("blue", "red"),
pch = c(19, 19))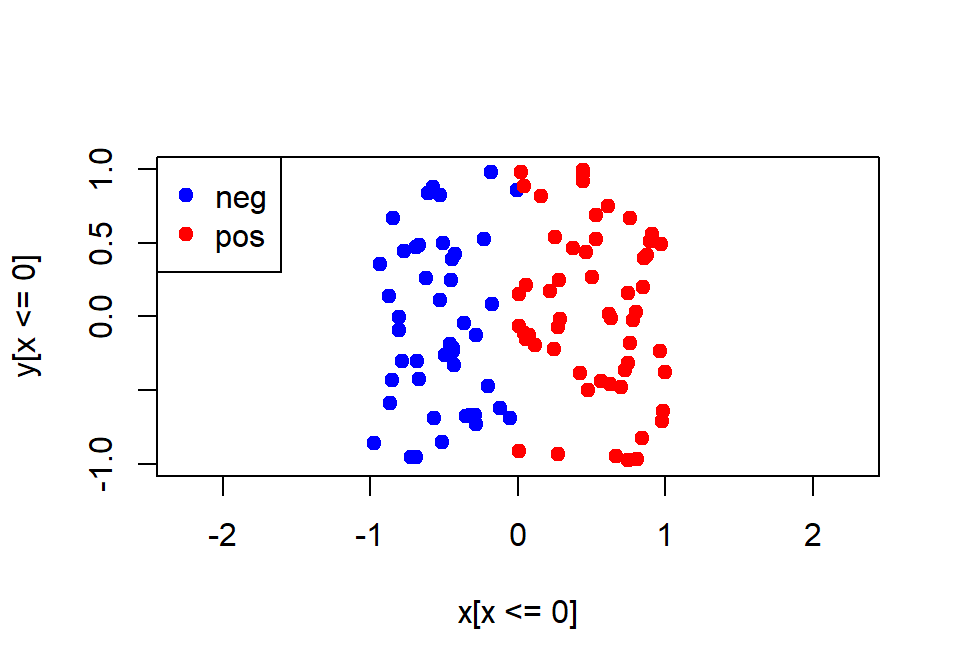
En un último ejemplo, más avanzado, mostramos un diagrama de dispersión de la longitud de pétalo, frente a su anchura para las flores del data frame iris. Los puntos se colorean según el factor Species.
plot(iris$Petal.Width, iris$Petal.Length, col = iris$Species, pch = 19)
legend("topleft", legend = levels(iris$Species), col = 1:3, pch = 19)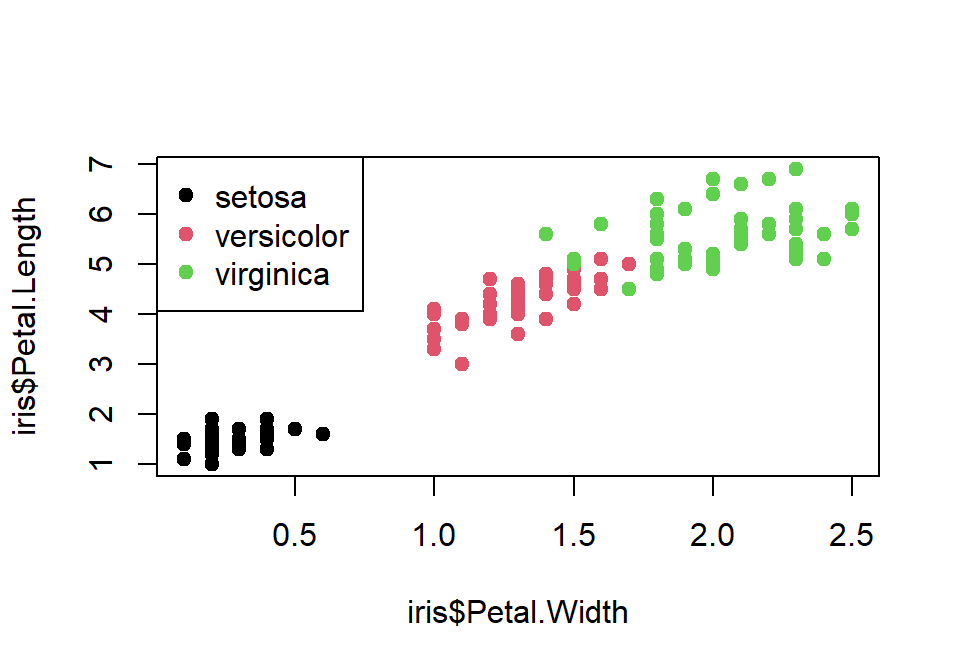
Los colores elegidos para dibujar los factores aparecen por orden en la salida de la función palette.
12.4 Histogramas: la función hist
La función hist produce un histograma del vector numérico que recibe como parámetro. El número de clases es seleccionado automáticamente, pero puede ser especificado, así como los límites de las clases. Por defecto se muestran las frecuencias, pero se puede seleccionar ver las frecuencias relativas.
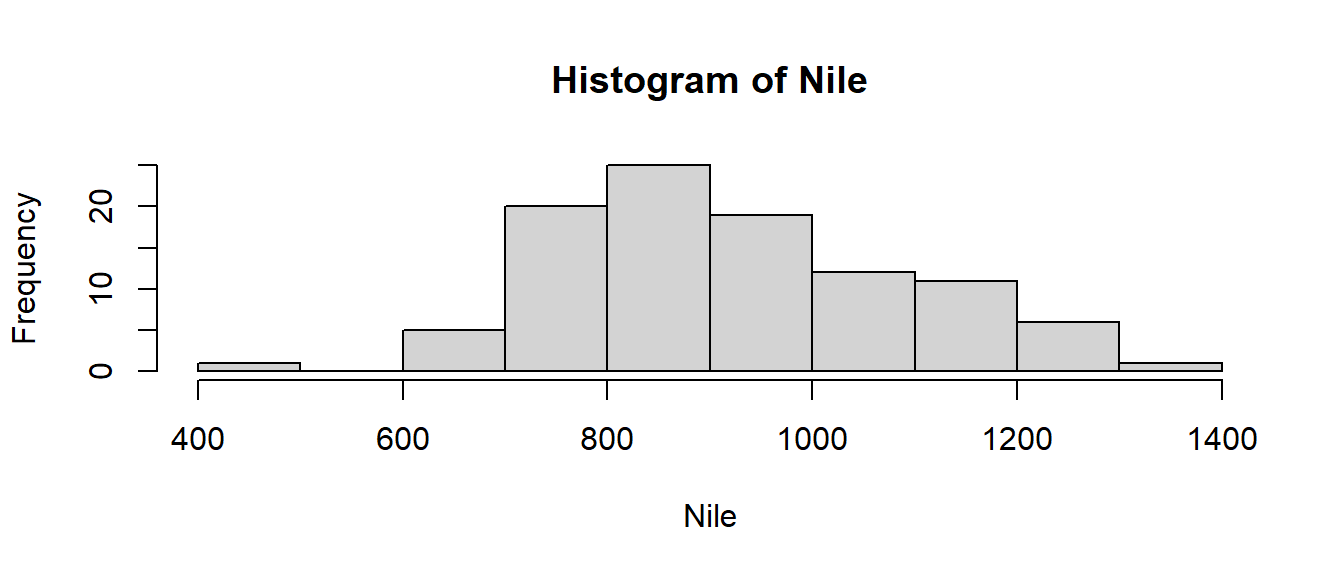
Veamos ahora un histograma con 15 clases y frecuencias relativas:
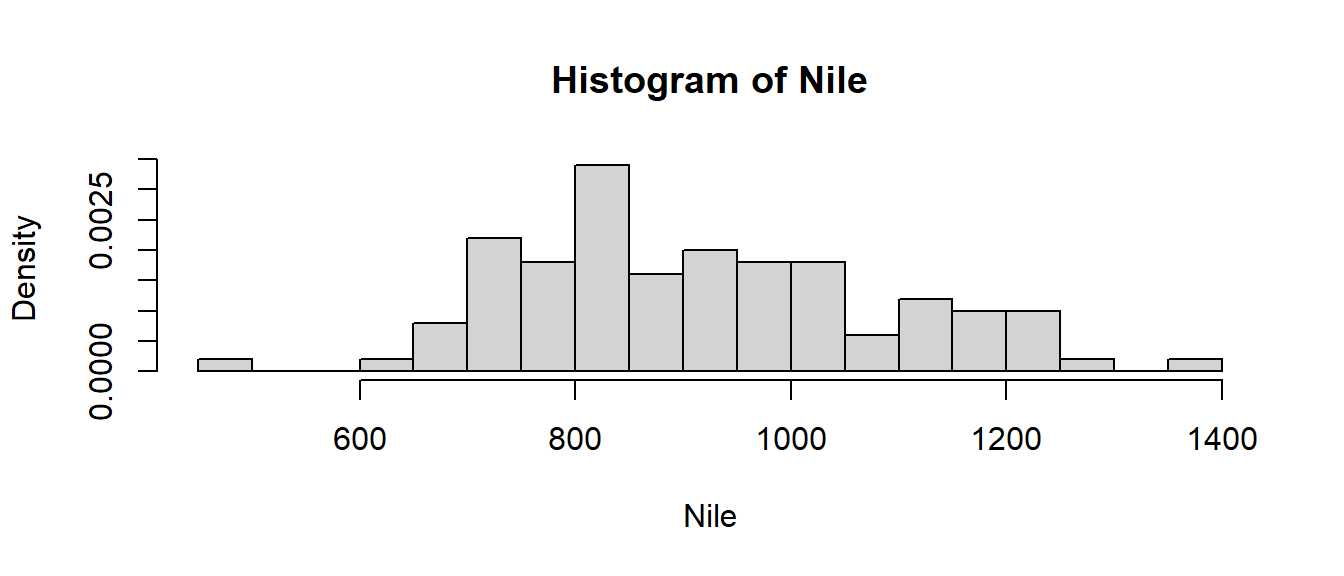
12.5 Diagramas de sectores: pie
Hemos visto que con barplot se puede obtener un gráfico de barras de los valores de una variable cualitativa. Con la función pie se puede obtener un diagrama de sectores.
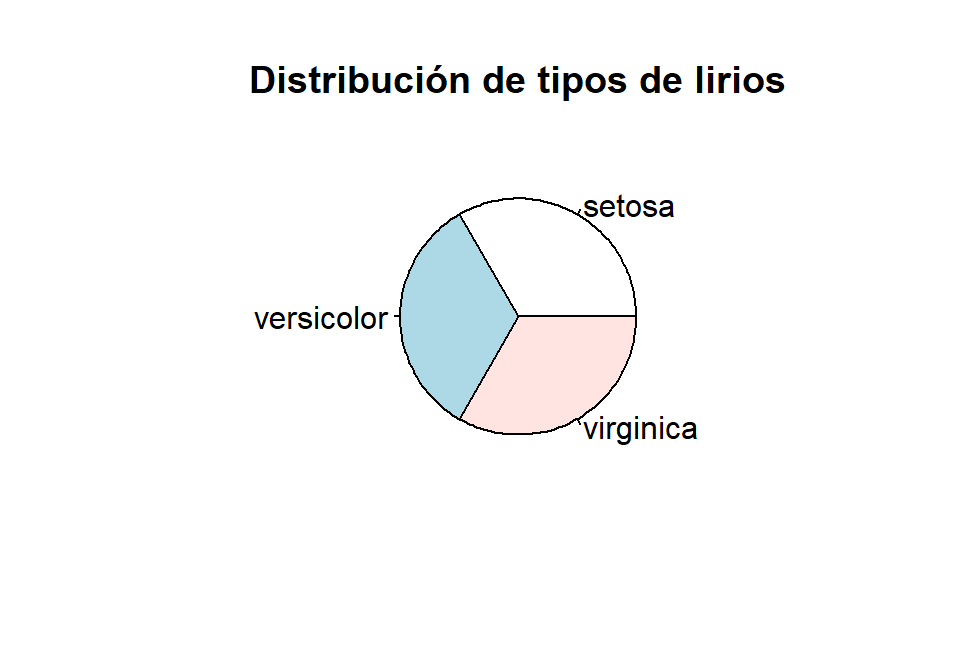
Es posible etiquetar cada sector. Por ejemplo, vamos a etiquetar cada tipo de lirio con su porcentaje de ocurrencias.
tabla <- prop.table(table(iris$Species))
pie(tabla,
main = "Distribución de tipos de lirios",
labels = paste(names(tabla), round(tabla*100, 2), "%")
)
12.6 Función locator y par
En esta sección se comentan dos funciones que pueden resultar útiles. La primera es la función locator. Esta función sirve para obtener las coordenadas de ciertos puntos en el gráfico. Al ejecutarla usaremos el ratón para posicionar el cursor en las coordenadas que nos interesan y pulsaremos el botón izquierdo tantas veces como coordenadas queramos obtener. Esta función resulta útil para saber aproximadamente qué coordenadas usar en una llamada a funciones como text o legend en las que podemos especificar una posición del gráfico donde ubicar un elemento. Como ejemplo, prueba lo siguiente en la consola:
A continuación sitúate en un punto del gráfico y pulsa el botón izquierdo del ratón.
La otra función es par, que sirve para especificar una serie de parámetros gráficos que se usan por defecto. Por ejemplo:
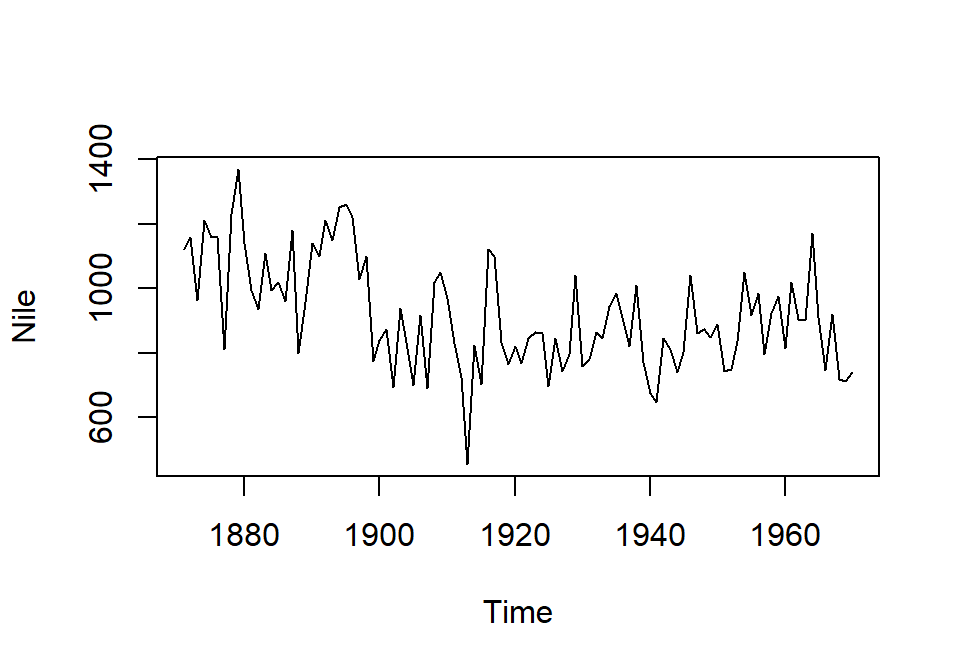
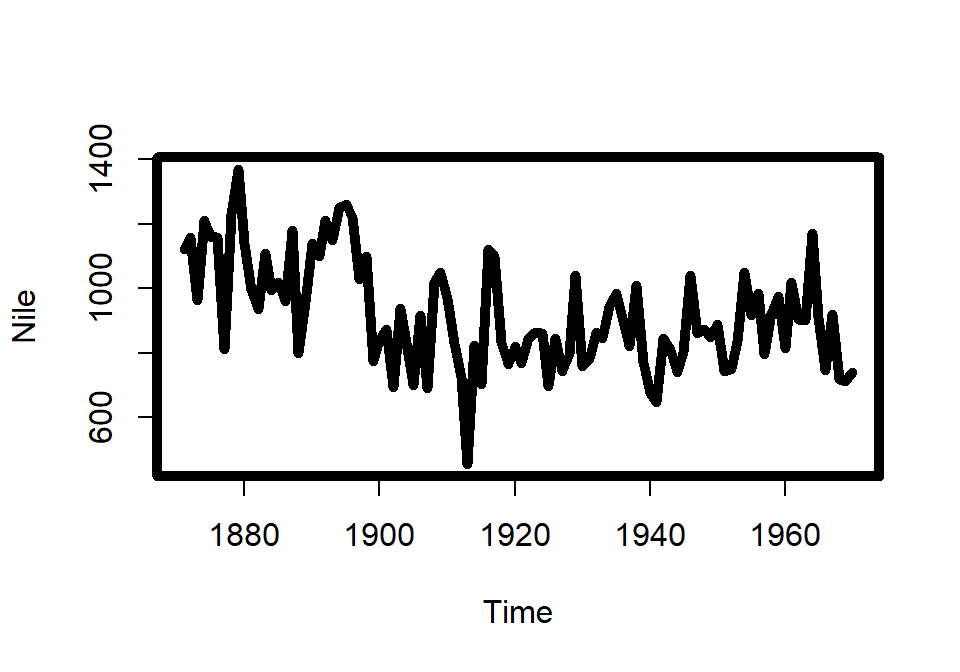
Si se usa sin parámetros, par devuelve una lista con los valores actuales de los parámetros por defecto. Un uso muy común es hacer que varios gráficos aparezcan en la misma pantalla:
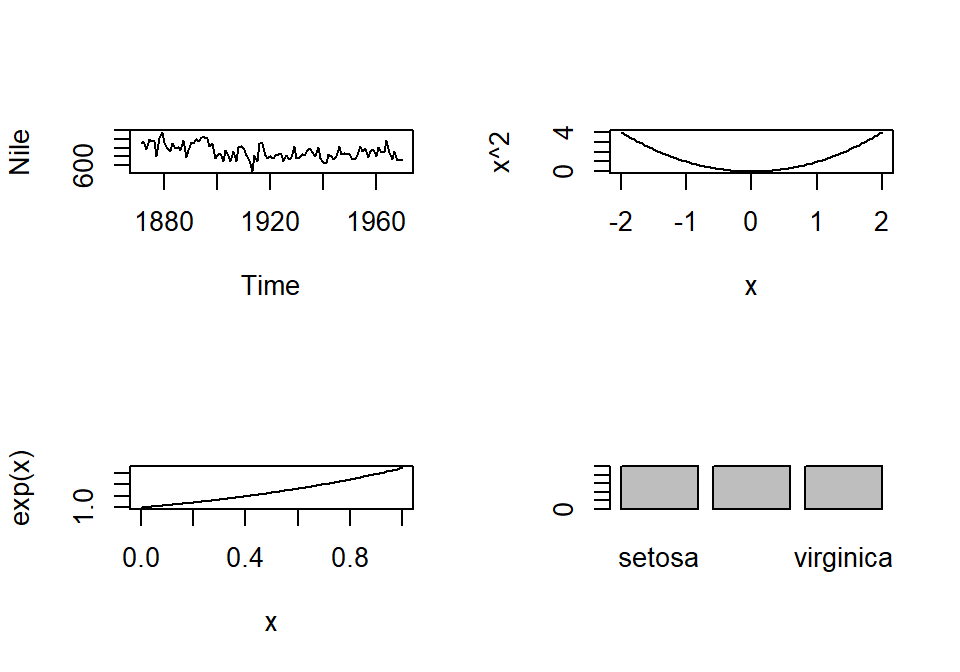
Si queremos restaurar el valor por defecto habrá que escribir par(mfrow = c(1, 1)).
12.7 Ejercicios
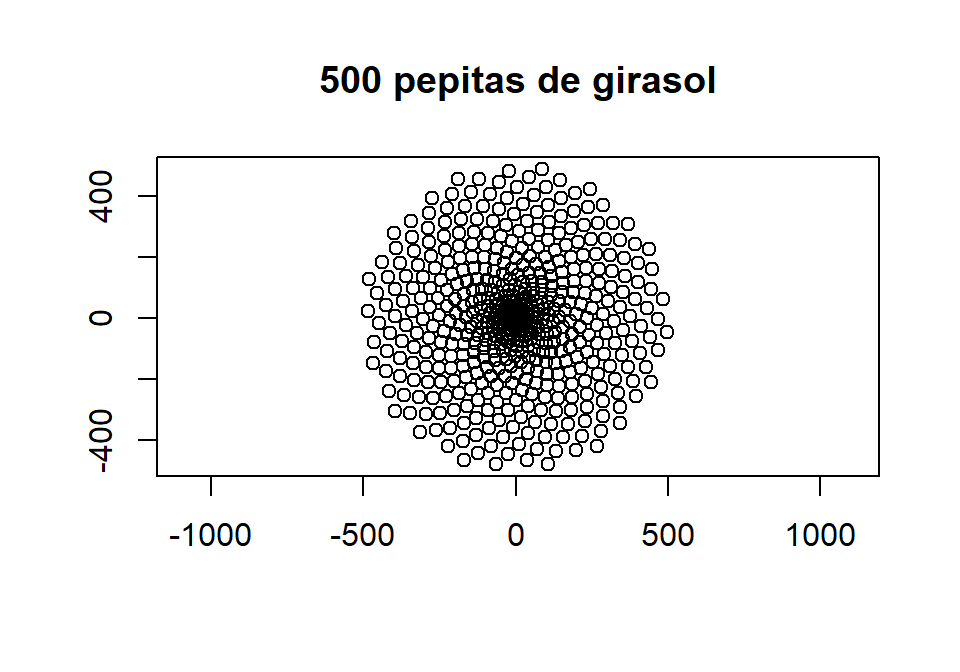
La disposición de las pepitas de un girasol sigue un modelo matemático. La \(n\)-ésima semilla tiene coordenadas polares \(r=\sqrt{n}\) y \(\alpha= \frac{137.51\pi n}{180}\). Escribe un programa que solicite el número de pepitas y las dibuje como círculos.
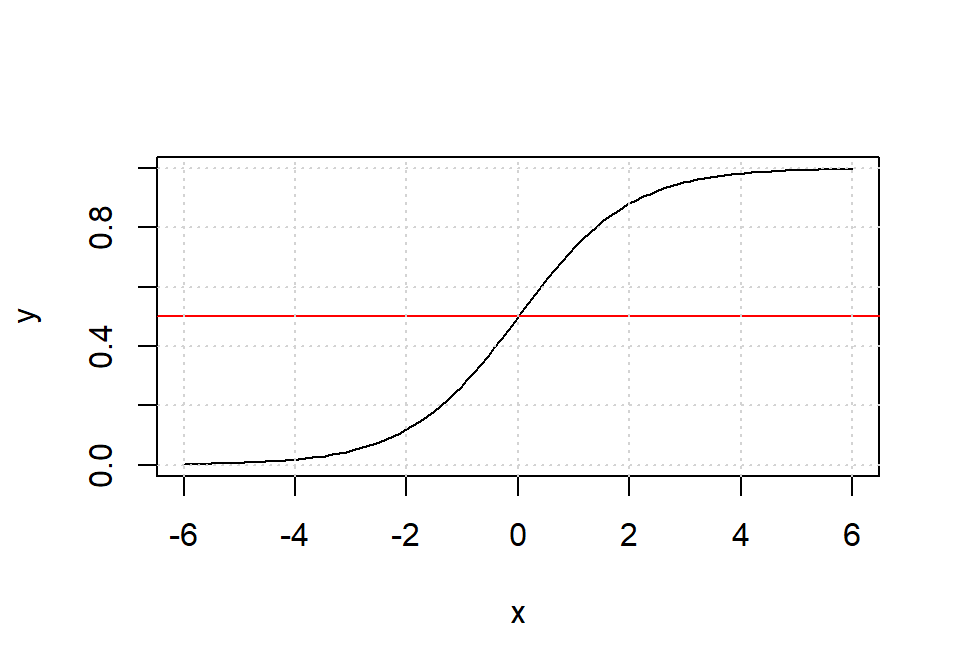
Representa la función logística simple:
\[P(t) = \dfrac{1}{1+ e^{-t}} \]
en el intervalo [-6, 6].
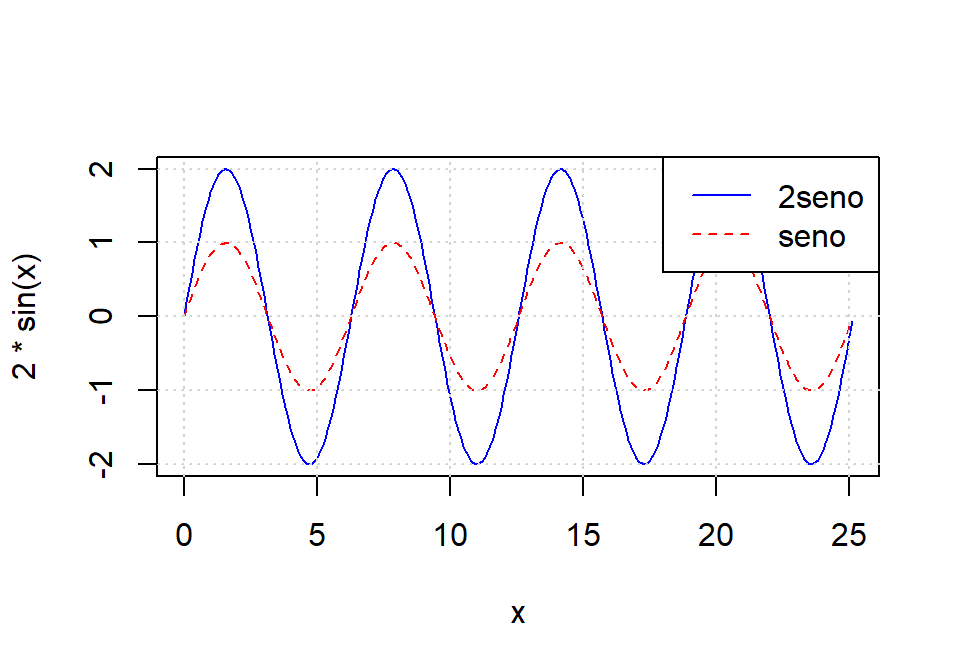
Representa las funciones \(\sin(x)\) y \(2\sin(x)\) en un mismo gráfico, etiquetando cada una de las funciones.
Genera 100 puntos aleatorios uniformemente distribuidos en el cuadrado de esquinas (-1, -1) y (1, 1). Dibuja los puntos de color negro. Dibuja de color rojo el punto más lejano al origen y une el origen y el punto con una línea roja. La distancia de un punto \((x, y)\) al origen se calcula como \(\sqrt{x^2 + y^2}\).

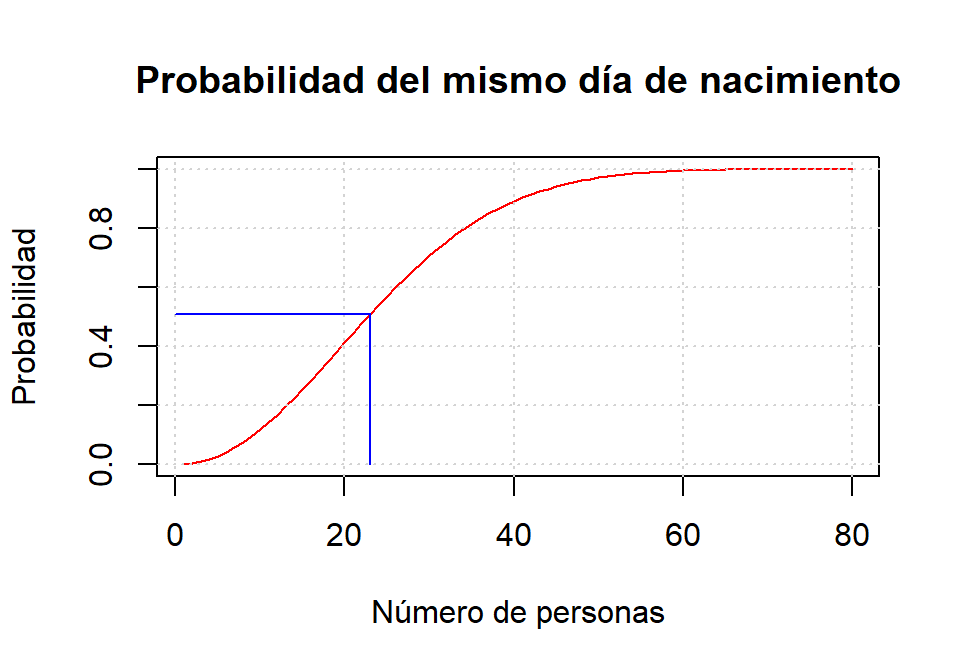
Supongamos que en una habitación se reunen n personas al azar, con \(n \leq 365\), y ninguna de ellas ha nacido el 29 de febrero, ni hay gemelos ni mellizos. La probabilidad de que al menos dos personas cumplan años el mismo día es:
\[ 1 - \frac{365}{365} \times \frac{364}{365} \times \frac{363}{365} \times \ldots \times \frac{365-n+1}{365} \]
Realiza una función que dado n devuelva la citada probabilidad. Como dato de prueba con 23 personas la probabilidad es 0.507. Haz un gráfico en el que se muestre cómo evoluciona la probabilidad en función del número de personas que haya en la habitación. Destaca en el gráfico la probabilidad para \(n = 23\) (ver siguiente gráfico).
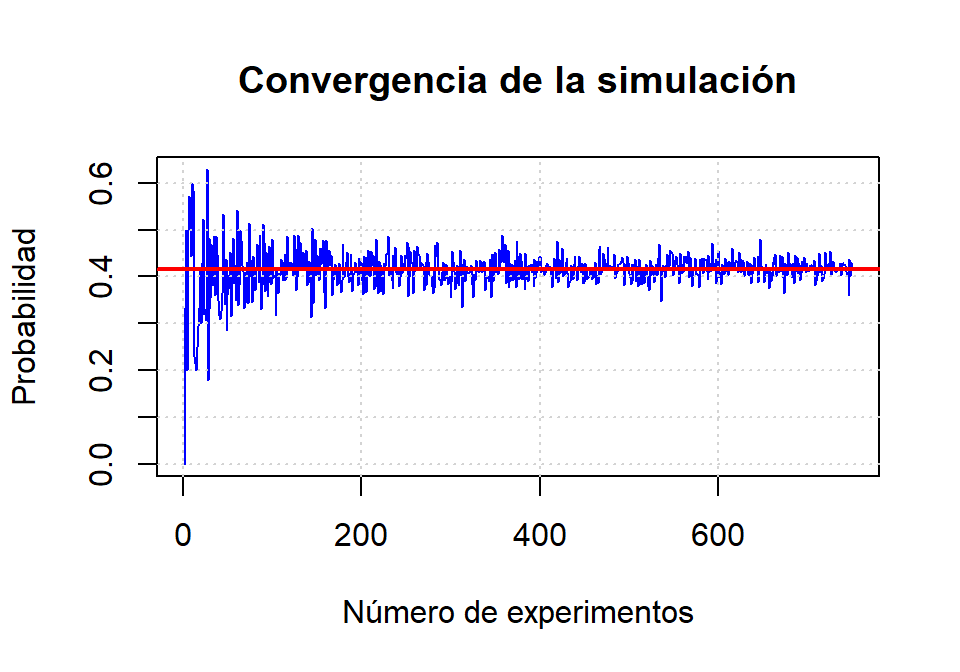
Supongamos que se lanzan dos dados, uno negro y otro verde, ¿Cuál es la probabilidad de que el dado negro tenga un valor mayor que el verde? En este caso la respuesta es sencilla: \(\frac{15}{36}\), porque hay 36 posibles combinaciones de los valores de los dos dados y en 15 de ellas el dado negro es mayor que el verde. Sin embargo, hay situaciones en las que no es posible o fácil hacer estos cálculos. En dichas situaciones se puede recurrir a una simulación en la que se repite N veces el experimento aleatorio y se calcula la proporción de veces en la que el experimento tiene éxito (en nuestro caso el éxito equivale a que el dado negro vale más que el verde). Esa proporción es una aproximación a la probabilidad buscada. Cuanto mayor sea N mayor confianza tenemos en el valor de la aproximación. De hecho, cuando \(N \to \infty\) se obtiene la solución exacta. Haz una función que calcule una aproximación a la probabilidad de que el dado negro sea mayor que el verde. Se puede escribir una función vectorizada que no use ciclos. El parámetro de la función es el valor de N. Haz una gráfica en la que se refleje cómo la simulación converge a \(\frac{15}{36}\).
Genera una matriz aleatoria con valores de 0 y 1. Por ejemplo:
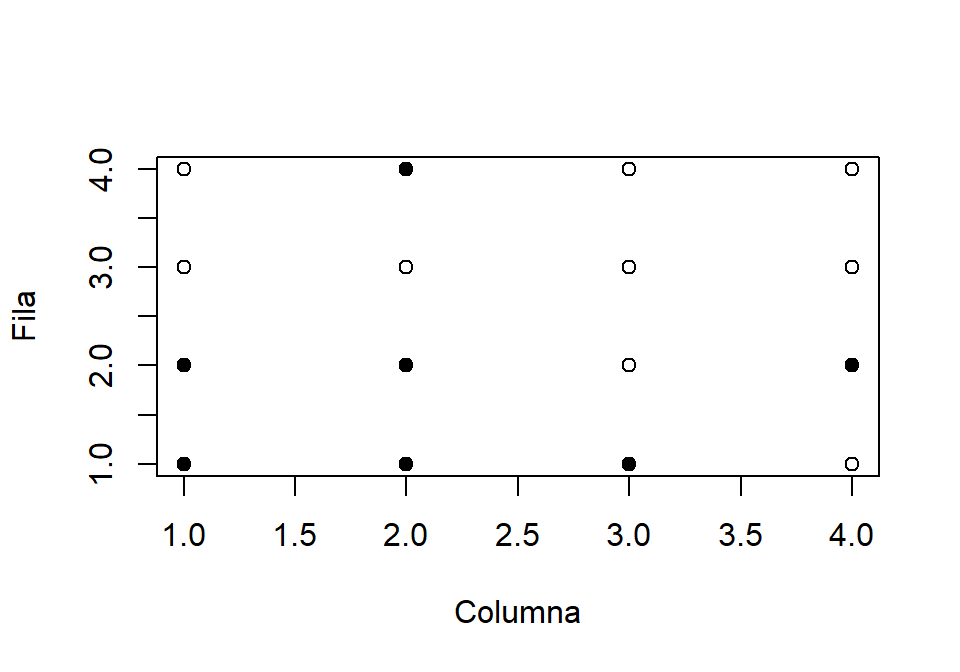
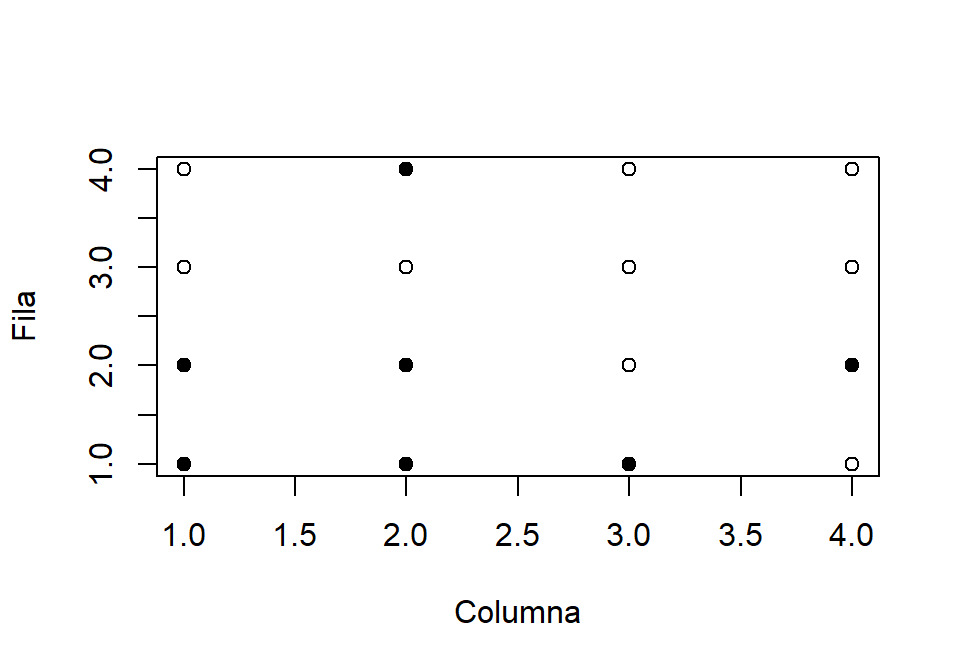
set.seed(10) (m <- matrix(sample(0:1, size = 16, replace = TRUE), nrow = 4)) ## [,1] [,2] [,3] [,4] ## [1,] 0 1 0 0 ## [2,] 0 0 0 0 ## [3,] 1 1 0 1 ## [4,] 1 1 1 0Representa la matriz gráficamente con distintos símbolos para el 0 y el 1. Por ejemplo:
12.8 Soluciones a los ejercicios
# Semillas de girasoles
n <- as.integer(readline("Número de semillas: "))
radio <- 1:n
angulos <- 137.51 * pi * 1:n / 180
x <- cos(angulos) * radio
y <- sin(angulos) * radio
plot(x, y, asp = 1)
# Función logística simple
t <- seq(-6, 6, length.out = 100)
plot(t, 1 / (1 + exp(-t)), type = "l", xlab = "x", ylab = "y")
abline(h = 0.5, col = "red")
grid()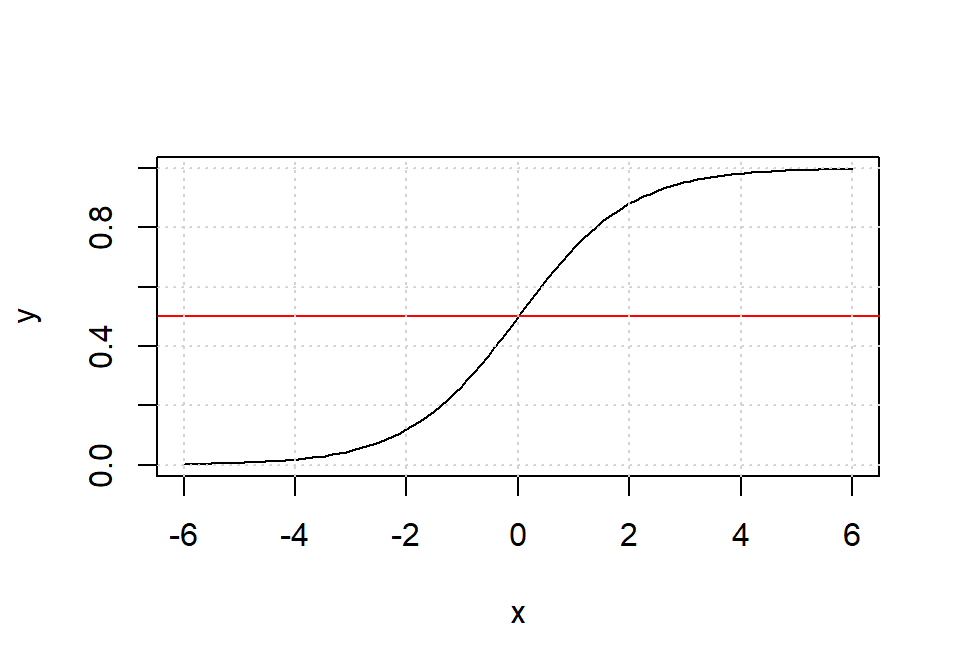
# Funciones seno
x <- seq(0, 8*pi, by = 0.1)
plot(x, 2*sin(x), type = "l", col = "blue")
lines(x, sin(x), col = "red", lty = "dashed")
grid()
legend("topright", legend = c("2seno", "seno"),
col = c("blue", "red"), lty = c("solid", "dashed"))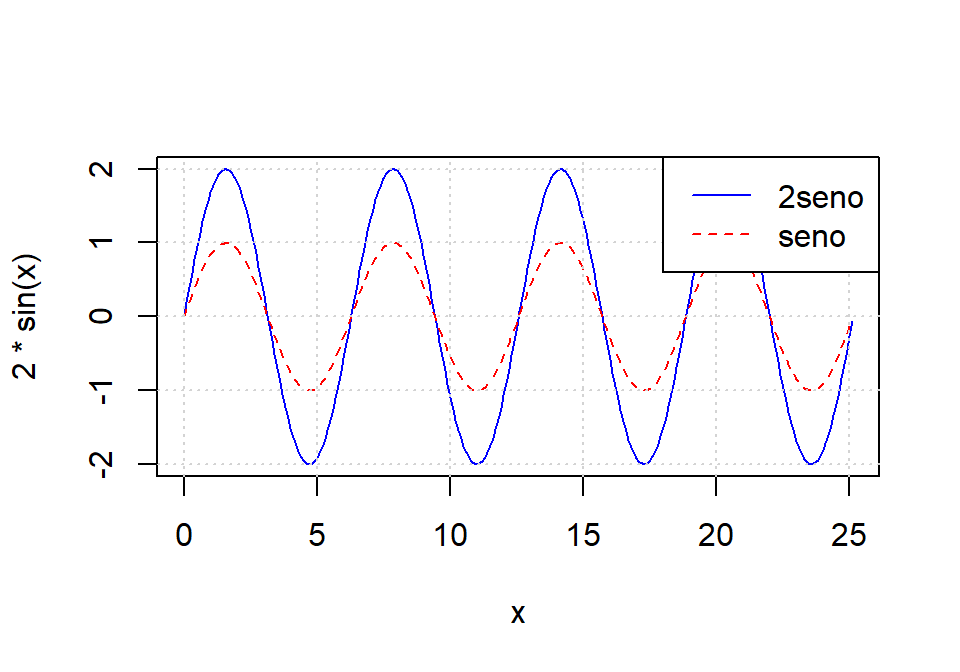
# Punto más lejano al origen
n <- 100
x <- runif(n, min = -1, max = 1)
y <- runif(n, min = -1, max = 1)
p_index <- which.max(x^2 + y^2)
plot(x, y, pch = 19, asp = 1)
points(c(0, x[p_index]), c(0, y[p_index]), pch = 19, col = "red")
lines(c(0, x[p_index]), c(0, y[p_index]), pch = 19, col = "red")
# Probabilidad cumpleaños el mismo día
prob <- function(n) {
producto <- 1
for (f in (365-n+1):365)
producto <- producto * f/365
1 - producto
}
p <- sapply(1:80, prob)
plot(1:80, p, type = "l", col = "red",
xlab = "Número de personas",
ylab = "Probabilidad",
main = "Probabilidad del mismo día de nacimiento")
grid()
lines(c(0, 23, 23), c(rep(prob(23), 2), 0), col = "blue")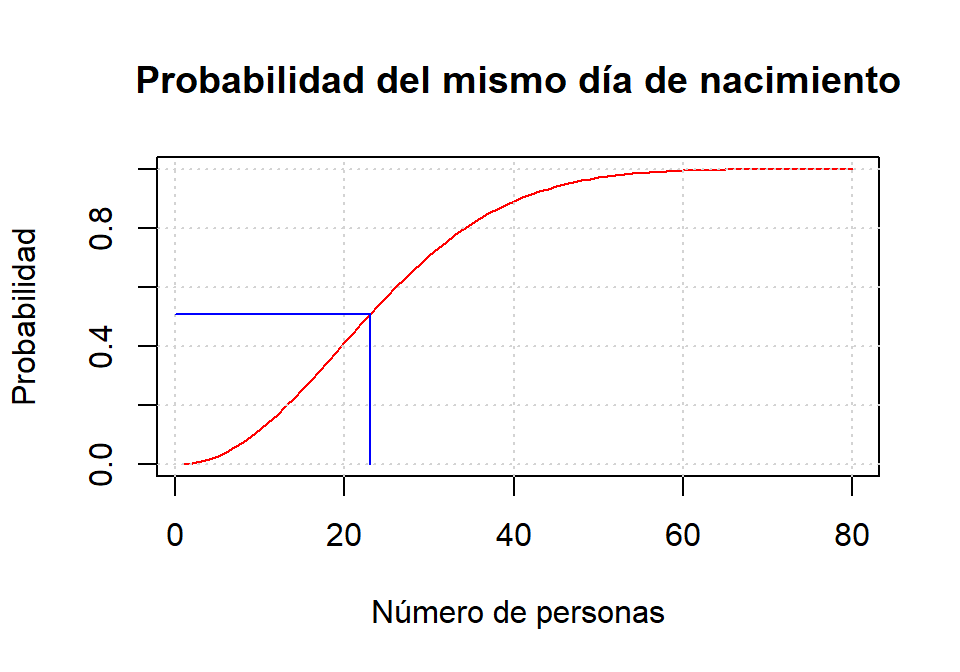
# Probabilidad cumpleaños el mismo día
prob <- function(n) {
producto <- 1
for (f in (365-n+1):365)
producto <- producto * f/365
1 - producto
}
p <- sapply(1:80, prob)
plot(1:80, p, type = "l", col = "red",
xlab = "Número de personas",
ylab = "Probabilidad",
main = "Probabilidad del mismo día de nacimiento")
grid()
lines(c(0, 23, 23), c(rep(prob(23), 2), 0), col = "blue")
# Convergencia simulación dado negro mayor que verde
prob <- function(n) {
negro <- sample(6, size = n, replace = TRUE)
verde <- sample(6, size = n, replace = TRUE)
mean(negro > verde)
}
p <- sapply(1:750, prob)
plot(1:750, p, type = "l", col = "blue",
xlab = "Número de experimentos",
ylab = "Probabilidad",
main = "Convergencia de la simulación"
)
grid()
abline(h = 15/36, col = "red", lwd = 2)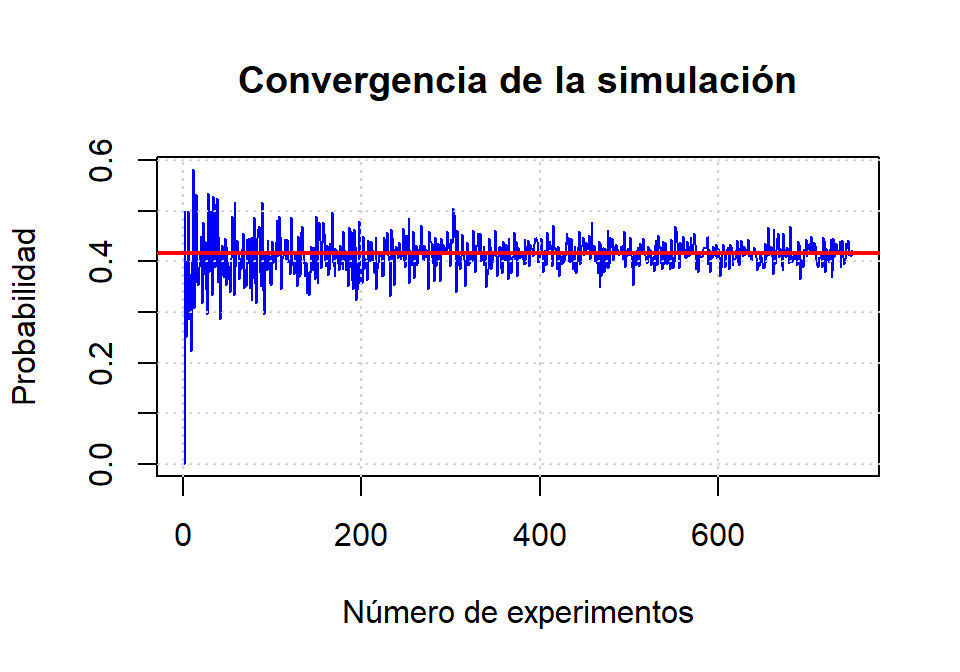
# Representación gráfica de una matriz de ceros y unos
set.seed(10)
m <- matrix(sample(0:1, size = 16, replace = TRUE), nrow = 4)
plot(1:ncol(m), 1:nrow(m), type = "n", xlab = "Columna", ylab = "Fila")
for (f in 1:nrow(m)) {
for (c in 1:ncol(m)) {
if (m[f, c] == 1) {
points(c, nrow(m)+1-f, pch = 19)
} else {
points(c, nrow(m)+1-f, pch = 1)
}
}
}