Página personal  de Miguel Ángel García Muñoz  Volver a principal  Volver a docencia

Asignatura: Matemáticas I

Grado en Ingeniería Geomática y Topográfica

La asignatura Matemática I está encuadrada dentro de la materia Matemáticas que a su vez forma parte del módulo de Formación básica del Grado en Ingeniería Geomática y Topográfica, año 2010. Esta asignatura es de carácter obligatorio y consta de 9 créditos ECTS que se dividen en 4.5 créditos de teoría (clases expositivas en grandes grupos) y 4.5 de prácticas (resolución de problemas en pizarra y prácticas con ordenador, en las que utilizando el software Mathematica se resolverán problemas relativos a la asignatura).

Guía docente de la asignatura 

Programación curso 2012/2013

PROGRAMA

Tema 1. Trigonometría plana y esférica ( pdf PowerPoint de clase)

Semejanza de triángulos. Medidas de ángulos. Razones trigonométricas. Obtención de razones trigonométricas: fórmulas y teoremas. Triángulos esféricos. Polar, área, altura esférica, resolución de triángulos esféricos, fórmulas de Bessel, analogías de Gauss-Delambre y Neper, pentágono de Neper

Tema 2. Algebra lineal ( pdf PowerPoint de clase)

Espacios Vectoriales, matrices, sistemas de ecuaciones lineales, diagonalización de matrices. Solución de una ecuación lineal, compatibilidad y determinación de un sistema de ecuaciones lineales, sistemas equivalentes, transformaciones elementales, método de Gauss, introducción de parámetros, los sistemas vistos como ecuaciones (las matrices, producto de matrices, inversa del producto de matrices, resolución de sistemas utilizando producto de matrices, determinantes, cálculo de la inversa por determinantes, regla de Cramer), los sistemas vistos como problemas de mezclas (los espacios vectoriales como ambiente para la suma y producto de elementos, combinación lineal, subespacios vectoriales, independencia lineal, generadores, base y dimensión), potencias de una matriz, vectores y valores propios, diagonalización de una matriz.
 

Tema 3.  Geometría analítica del plano y del espacio ( pdf PowerPoint de clase)

Cónicas y cuádricas. Punto, vector, distancia, producto escalar, ecuaciones de la recta, ángulos entre rectas, ecuaciones del plano, producto vectorial, posiciones relativas. Cónicas en posición estándar, elementos de las cónicas, reducción de una cónica a posición estándar, cuádricas, introducción a la clasificación de cuádricas.
 

Tema 4. Calculo diferencial e integral para funciones de una variable ( pdf PowerPoint de clase)

Introducción a las funciones reales, límites y continuidad, asíntotas, derivabilidad, cálculo de derivadas, crecimiento, convexidad, máximos y mínimos, absolutos y relativos, optimización, integración definida e indefinida, aplicaciones, cálculo de áreas, longitudes y volúmenes.
 

Tema 5. Calculo diferencial e integral para funciones de varias variables ( pdf PowerPoint de clase)

Funciones de varias variables, representación gráfica de funciones de varias variables, derivación parcial, integración múltiple.
 

Tema 6. Métodos numéricos ( pdf PowerPoint de clase) (VER PRÁCTICAS)

El porqué de los métodos numéricos, interpolación polinomial, aproximación mínimos cuadrados, resolución numérica de ecuaciones no lineales, derivación e integración numérica, introducción a los métodos numéricos del álgebra lineal.
 

Tema 7. Estadística descriptiva ( pdf PowerPoint de clase)

Variable estadística, parámetro estadístico, Medidas de tendencia central (media, mediana, moda, cuartiles, deciles, percentiles), Medidas de dispersión (rango, desviación media, desviación mediana, varianza, desviación típica), Medidas de asimetría, Medidas de apuntamiento, Estadística bidimensional (centro de gravedad, Covarianza, recta de regresión, correlación. Coeficiente de correlación de Pearson).

BIBLIOGRAFÍA

Todos estos títulos puedes encontrarlos en la Biblioteca de la Universidad de Jaén

ESPECÍFICA O BÁSICA:

• Teoría y problemas de trigonometría: plana y esférica. Edición: -. Autor: Ayres, Frank. Editorial: Mexico ; Madrid [etc.]: McGraw-Hill, imp. 1990  (C. Biblioteca)
• Algebra lineal: con métodos elementales. Edición: 2ª reimp.. Autor: Merino González, Luis M.. Editorial: Madrid : Thomson, 2007.  (C. Biblioteca)
• Algebra y geometría analítica. Edición: -. Autor: Granero Rodríguez, Francisco. Editorial: Madrid [etc.]: McGraw-Hill, D.L. 1994  (C. Biblioteca)
• Cálculo. Edición: 9ª ed. Autor: Larson, Ron (1941-). Editorial: México : McGraw Hill, 2010  (C. Biblioteca)
• Análisis númerico. Edición: 7ª ed. Autor: Burden, Richard L.. Editorial: México: International Thomson Editores, imp. 2003  (C. Biblioteca)
• Probabilidad y estadística para ingeniería y ciencias. Edición: 4ª ed. Autor: Mendenhall, William. Editorial: México [etc.]: Prentice-Hall Hispanomericana, 1997  (C. Biblioteca)

GENERAL Y COMPLEMENTARIA:

• Álgebra lineal. Edición: 6ª ed.. Autor: Grossman, Stanley I.. Editorial: México : MacGraw-Hill, 2008.  (C. Biblioteca)
• Cálculo con geometría analítica. Edición: 4ª ed. Autor: Edwards, C. H.. Editorial: México[etc.]: Pearson Educación, cop. 1996  (C. Biblioteca)
• Cálculo diferencial e integral. Edición: 3ª ed. Autor: Ayres, Frank. Editorial: México [etc.]: McGraw-Hill, imp. 2000  (C. Biblioteca)
• Problemas de álgebra lineal: cuestiones, ejercicios y tratamiento en DERIVE. Edición: Última reimp. Autor: Sanz, Paloma. Editorial: Madrid: Prentice Hall, 2002  (C. Biblioteca)
• Métodos computacionales en álgebra para informáticos: matemática discreta lógica. Edición: -. Autor: García Muñoz, Miguel A.. Editorial: [Jaén]: Área de Álgebra, Universidad de Jaén, [2006]  (C. Biblioteca)
• Análisis y métodos numéricos: Ingeniería Técnica en Informática de Gestión. Edición: -. Autor: -. Editorial: [Jaén] : Universidad de Jaén , [2004]  (C. Biblioteca)

PRÁCTICAS

La parte práctica de la asignatura se basa en la resolución de problemas afines a la asignatura y se divide en dos partes:

    (A) Resolución en pizarra de problemas de las relaciones propuestas

RELACIONES DE PROBLEMAS
1.-	RELACIÓN DE PROBLEMAS DEL TEMA 1
2.-	RELACIÓN DE PROBLEMAS DEL TEMA 2
3.-	RELACIÓN DE PROBLEMAS DEL TEMA 3   Ejercicios resueltos de geometría analítica en el espacio (pdf)
4.-	RELACIÓN DE PROBLEMAS DEL TEMA 4
5.-	RELACIÓN DE PROBLEMAS DEL TEMA 5
6.-	RELACIÓN DE PROBLEMAS DEL TEMA 6
7.-	RELACIÓN DE PROBLEMAS DEL TEMA 7

 

    (B) Resolución de problemas con ayuda del ordenador utilizando el software Mathematica.

SISTEMA DE EVALUACIÓN

El desarrollo teórico tendrá lugar durante 3 horas semanales (lunes de 16:30 a 17:30 y miércoles de 15:30 - 17:30) en las que el profesor explicará los contenidos de la asignatura y realizará ejemplos prácticos de estos contenidos. En estas clases el alumno deberá atender a las explicaciones y tomar apuntes que complemente el material facilitado por el profesor. La asistencia y participación del alumno a estas clases es muy aconsejable, así como llevar la asignatura al día y consultar cuantas dudas surjan, tanto en clase como en el horario de tutorías del profesor.

Además el alumno tendrá una hora semanal de problemas (jueves de 18:30 a 19:30) que se dedicarán a resolver en la pizarra problemas de las relaciones que previamente ha facilitado el profesor y dos horas semanales dedicadas a prácticas de ordenador en grupos reducidos de 40 alumnos. en las que aprenderemos el manejo del software Mathematica, el cual lo utilizaremos para resolver de una forma rápida los problemas que previamente se han realizado en clase, con lo cual el propio alumno puede corregir y reafirmar aquellos problemas o conceptos que no quedaron lo suficientemente claros.

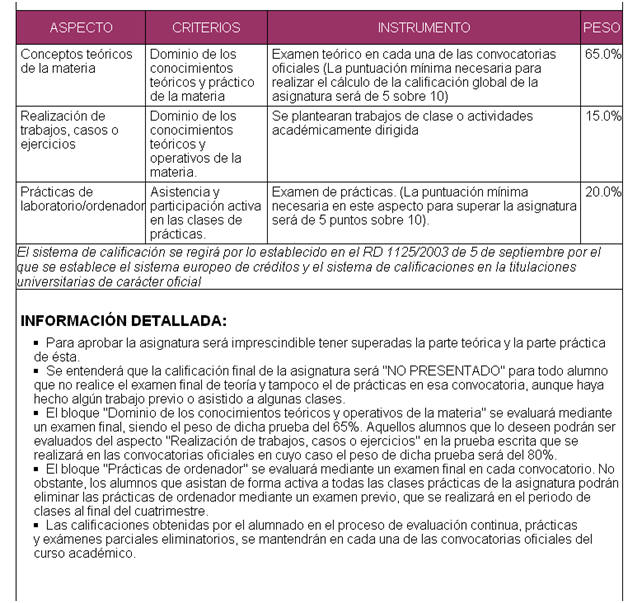
La calificación se obtendrá a partir de un examen escrito con un valor del 80%, y un examen de prácticas en las aulas de ordenador que se evaluará con un valor de 20%.  Este examen de prácticas tendrá lugar el mismo día de la convocatoria oficial. No obstante, para facilitar el aprobado en las prácticas el alumno puede optar por un ejercicio durante el periodo académico y en el horario de clase. Para acceder a este tipo de evaluación será requisito indispensable la asistencia activa a las sesiones de prácticas, entendiendo por activa que el alumno vaya trabajando los distintos problemas propuestos por el profesor, para ello el profesor podrá pedir las prácticas ya realizadas semanalmente. El alumno que apruebe las prácticas, tendrá esta calificación para cualquier convocatoria del mismo curso académico. Por otra parte, el profesor podrá proponer trabajos que podrían evaluarse entre el 0% y el 15% de la valoración del examen escrito y según las actividades superadas.

Fechas de examen

Alumnos que han superado algún tema con los trabajos realizados

como actividad académica dirigida (Jmathwiki)

Convocatoria enero:

Jueves, 24 de enero de 2013

Aulas:  34      Edificio: A4

Horario: 9:00

Calificaciones examen final febrero (Grupo B)

El alumno con DNI 77371797 ha superado las prácticas en la convocatoria de enero con un 7. Esta calificación se le guardará para las siguientes convocatorias de este curso.

La revisión del examen será el próximo viernes 1 de febrero a las 12:00 en el despacho del profesor (016-B3)

Convocatoria mayo/junio:

Lunes, 20 de mayo de 2013

Aulas:        Edificio:

Horario: 

Calificaciones examen final junio

Convocatoria junio/julio:

Lunes, 24 de junio de 2013

Aulas:                Edificio:

Horario:

Calificaciones examen convocatoria extraordinaria 2

La revisión del examen será el próximo viernes 5 de julio a las 12:00 en el despacho del profesor (016-B3)

EXÁMENES DE AÑOS ANTERIORES
2013/14	Examen JUNIO/JULIO 2014 ( pdf) Examen MAYO/JUNIO 2014 ( pdf) Examen ENERO 2014 ( pdf)	2012/13	Examen JUNIO/JULIO 2013 ( pdf) Examen MAYO/JUNIO 2013 ( pdf) Examen ENERO 2013 ( pdf)
2011/12	Examen SEPTIEMBRE 2012 ( pdf) Examen JUNIO 2012 ( pdf) Examen FEBRERO 2012 ( pdf)	2010/11	Examen SEPTIEMBRE 2011 ( pdf) Examen JUNIO 2011 ( pdf) Examen FEBRERO 2011 ( pdf)

Miguel Ángel García Muñoz

Universidad de Jaén

Departamento de Matemáticas

magarcia ujaen.es

Tfn: +34 953212935