Página personal  de Miguel Ángel García Muñoz  Volver a principal  Volver a docencia

Asignatura: Álgebra

Grado en Estadística y Empresa

La asignatura Álgebra está encuadrada dentro de la materia Matemáticas que a su vez forma parte del módulo de Formación básica del Grado en Estadística y Empresa, año 2010. Esta asignatura es de carácter obligatorio y consta de 6 créditos ECTS que se dividen en 3 créditos de teoría (clases expositivas en grandes grupos) y 3 de prácticas (resolución de problemas en pizarra y prácticas con ordenador, en las que utilizando el software Mathematica se resolverán problemas relativos a la asignatura).

Guía docente de la asignatura 

Programación curso 2012/2013

PROGRAMA

Tema 1. Sistemas de ecuaciones lineales. Matrices y determinantes ( pdf PowerPoint de clase)

Sistemas de ecuaciones lineales. Método de Gauss-Jordan. Matrices y sistemas de ecuaciones lineales. Forma normal de Hermite. Rango de una matriz. Teorema de Rouché-Fröbenius. Matrices elementales. Matrices inversas. Determinantes y algunas aplicaciones.

Tema 2. Espacios vectoriales y espacio vectorial euclideo ( pdf PowerPoint de clase)

Espacio vectorial. Dependencia e independencia lineal. Bases y dimensión. Subespacios vectoriales y operaciones con subespacios. Producto escalar y norma. Vectores ortogonales.  

Tema 3.  Aplicaciones lineales ( pdf PowerPoint de clase)

Aplicaciones lineales. Núcleo e imagen. Expresión matricial de un homomorfismo. Clasificación de una aplicación lineal.

Tema 4. Diagonalización ( pdf PowerPoint de clase)

Valores y vectores propios de un endomorfismo. Polinomio característico. Diagonalización de un endomorfismo por semejanza. Descomposición en valores singulares. Aplicaciones.

Tema 5. Inversas generalizadas ( pdf PowerPoint de clase)

Inversas laterales. Inversa generalizada de Moore-Penrose. Factorización de rango pleno. Solución mínimo cuadrática de norma mínima.

Información Actividad Académicamente Dirigida (voluntaria)

BIBLIOGRAFÍA

Todos estos títulos puedes encontrarlos en la Biblioteca de la Universidad de Jaén

ESPECÍFICA O BÁSICA:

1. MERINO, L. Y SANTOS, E., "Álgebra lineal con métodos elementales”. Ed. Thomson-Paraninfo, 2006. ISBN:84-9732-481-1

2. BARRIOS GARCÍA, J. A., GONZÁLEZ, C. Y MORENO PIQUERO, J. C., "Álgebra matricial para economía y empresa". Ed. Delta Publicaciones, 2006.

3. ANTON, H., "Introducción al Álgebra Lineal". Ed. Limusa, 1998.

4. BARBOLLA, R., SANZ P., "Álgebra lineal y teoría de matrices". Ed. Prentice Hall, 1998.

5. GRANERO RODRIGUEZ, F. "Álgebra y Geometría analítica". Ed. McGraw Hill, 1985.

GENERAL Y COMPLEMENTARIA:

1. ANTÓN, “Intoducción al álgebra lineal”. Ed. Limusa, 1990. ISBN: 0-7-471-05338-4.

2. ANZOLA, M. Y OTROS. "Problemas de Álgebra: Espacios vectoriales" (tomo 3). Ed. Autores, 1981/82

3. ARVESÚ, J., MARCELLÁN, F., SÁNCHEZ, J. "Problemas resueltos de Álgebra Lineal". Ed. Thomson. 2005.

4. BURGOS, J. DE. "Álgebra Lineal". Ed. McGraw Hill. 1995.

5. CRIADO, R. y OTROS. “Álgebra lineal: Método, fundamentos y algoritmos”. Ed. AC, 1993.

6. DIEGO, B., GORDILLO, E., VALEIRAS, G., "Problemas de Álgebra lineal”. Ed. Deimos.

7. GARCÍA GARCÍA, J., LÓPEZ PELLICER, M. "Álgebra lineal y Geometría. Ejercicios". Ed. Marfil, 1991.

8. GROSSMAN, S., “Álgebra lineal”. Ed. Mc Graw-Hill, 1996.

9. ROJO, J. y MARTÍN, I. "Ejercicios y problemas de Álgebra lineal". Ed. McGraw – Hill, 1996.

10. SANCHEZ, R., “Ejercicios y problemas de Álgebra lineal”. ICE. Universidad de Granada, 1990.

11. SANZ, P., “Problemas de álgebra lineal: cuestiones, ejercicios y tratamiento en Derive”, Prentice Hall, 1998.

12. VILLA, A. de la, “Problemas de Álgebra”. Ed. Glagsa, 1994.

13. BLACHMAN, N. "Mathematica". Ed. Addison-Wesley, 1992.

14. BLACHMAN, N. "Mathematica. Un enfoque práctico". Ariel Informática, 1993.

15. DOMINGUEZ PEREZ, J.A. Y OTROS, “Algebra  lineal. Planteamiento y resolución de problemas con Mathematica”. Ed. Plaza Universitaria, Salamanca, 1995.

16. FERNANDEZ – FERREIROS, A. y OTROS, "Álgebra lineal. Prácticas con Mathematica". Ed. Prensas Universitarias de Zaragoza, Zaragoza, 1995

17. GARCÍA-MUÑOZ, M.A., ORDOÑEZ, C. Y RUIZ, J.F., "Métodos computacionales en álgebra para informáticos. Matemática discreta y lógica". Ed. Servicio de publicaciones de la UJA, 2006.

18. RAMÍREZ GONZÁLEZ, V. Y OTROS "Matemáticas con Mathematica". Granada: Proyecto Sur de ediciones, 1996.

19. WOLFRAM, S. “Mathematica. A System for Doing Mathematics by Computer”. Addison-Wesley, 1991.

PRÁCTICAS

La parte práctica de la asignatura se basa en la resolución de problemas afines a la asignatura y se divide en dos partes:

    (A) Resolución en pizarra de problemas de las relaciones propuestas

    (B) Resolución de problemas con ayuda del ordenador utilizando el software Mathematica.

SISTEMA DE EVALUACIÓN

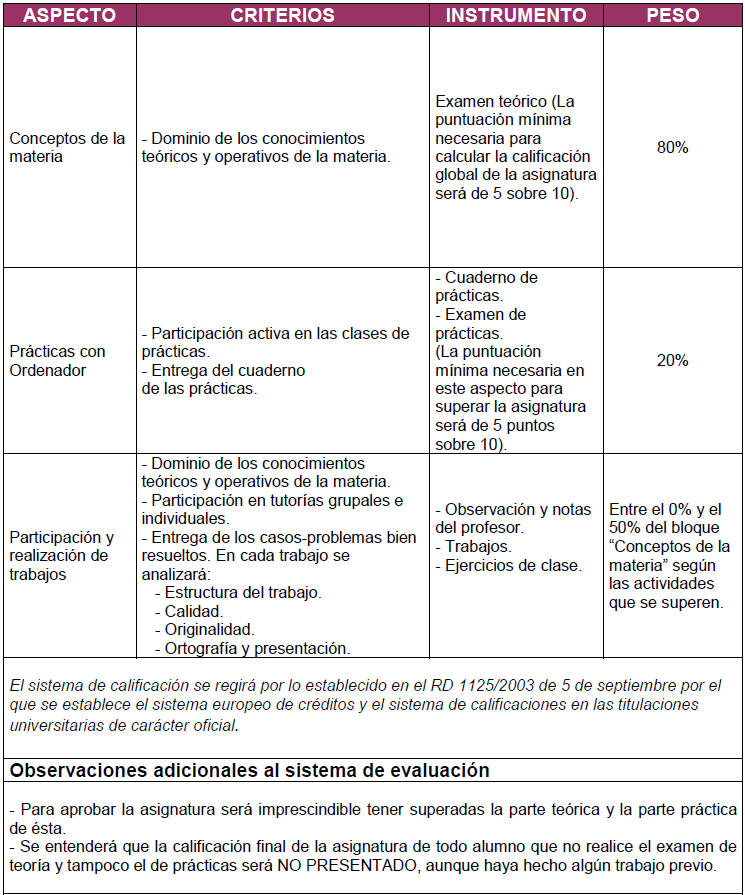
El desarrollo teórico tendrá lugar durante 2 horas semanales (martes y jueves de 9:30 - 10:30) en las que el profesor explicará los contenidos de la asignatura y realizará ejemplos prácticos de estos contenidos. En estas clases el alumno deberá atender a las explicaciones y tomar apuntes que complemente el material facilitado por el profesor. La asistencia y participación del alumno a estas clases es muy aconsejable, así como llevar la asignatura al día y consultar cuantas dudas surjan, tanto en clase como en el horario de tutorías del profesor.

Además el alumno tendrá dos horas semanales dedicadas a prácticas en grupos reducidos de 40 alumnos. Aproximadamente el 50% de estas horas se dedicarán a resolver en la pizarra problemas de las relaciones que previamente ha facilitado el profesor. Respecto a las clases prácticas con ordenador, aprenderemos el manejo del software Mathematica, el cual lo utilizaremos para resolver de una forma rápida los problemas que previamente se han realizado en clase, con lo cual el propio alumno puede corregir y reafirmar aquellos problemas o conceptos que no quedaron lo suficientemente claros.

La calificación se obtendrá a partir de un examen escrito con un valor del 80%, y un examen de prácticas en las aulas de ordenador que junto con el cuaderno de prácticas realizado durante el curso se evaluará con un valor de 20%.  Este examen de prácticas tendrá lugar el mismo día de la convocatoria oficial. No obstante, para facilitar el aprobado en las prácticas el alumno puede optar por un ejercicio durante el periodo académico y en el horario de clase. Para acceder a este tipo de evaluación será requisito indispensable la asistencia activa a las sesiones de prácticas, entendiendo por activa que el alumno vaya trabajando el cuaderno durante cada clase, para ello el profesor podrá pedir las prácticas ya realizadas semanalmente. El alumno que apruebe las prácticas, tendrá esta calificación para cualquier convocatoria del mismo curso académico. Por otra parte, el profesor podrá proponer trabajos que podrían evaluarse entre el 0% y el 50% de la valoración del examen escrito y según las actividades superadas.

Fechas de examen

Alumnos que han superado algún tema con los trabajos realizados

como actividad académica dirigida (Jmathwiki)

Convocatoria enero:

Martes, 22 de enero de 2013

Aulas:  23    Edificio:   A4

Horario: 9:00

Calificaciones examen final enero

La revisión del examen será el próximo jueves 31 de enero a las 12:00 en el despacho del profesor (016 - B3)

Convocatoria mayo/junio:

Lunes, 3 de junio de 2013

Aulas:        Edificio:

Horario: 

Calificaciones examen final junio

La revisión del examen será el próximo miércoles 12 de junio a las 12:00 en el despacho del profesor (016 - B3)

Convocatoria junio/julio:

Miércoles, 3 de julio de 2013

Aulas:                Edificio:

Horario:

Calificaciones examen final septiembre

La revisión del examen será el próximo miércoles 10 de julio a las 12:00 en el despacho del profesor (016 - B3)

EXÁMENES DE AÑOS ANTERIORES
2012/13	Examen JUNIO/JULIO 2013 ( pdf) Examen MAYO/JUNIO 2013 ( pdf) Examen ENERO 2013 ( pdf)	2011/12	Examen SEPTIEMBRE 2012 ( pdf) Examen JUNIO 2012 ( pdf) Examen FEBRERO 2012 ( pdf)

Miguel Ángel García Muñoz

Universidad de Jaén

Departamento de Matemáticas

magarcia @ ujaen.es

Tfn: +34 953212935