La ecuación de Clairaut

 

 

 

David Molina Muñoz

Diplomatura de Estadística + Ingeniería Técnica en Informática de Gestión

Fecha: 19 / Octubre / 2006

Índice

 

 

      Contenido                                   Pág. (s)

 

Introducción...................................................................... 2

 

Conceptos previos............................................................ .3

 

Desarrollo...................................................................... 4 – 5

 

Ejemplo............................................................................... 6

 

Biografía de Alexis-Claude Clairaut........................ 7 – 9

 

Bibliografía....................................................................... 10

 

                                                                  

 

 

 

 

 

 

 

 

 

 

 

 

 

Introducción

 

 

La ecuación de Clairaut, llamada así por su inventor, el físico francés Alexis-Claude Clairaut, es una ecuación diferencial de la forma:

 

y = xy’ + g(y’)

 

donde g(x) es una función continuamente diferenciable.

 

El interés que presenta este tipo de ecuación se debe al hecho de que tiene como solución a una familia de rectas. Además, la envolvente, es decir, la curva cuyas tangentes están dadas por la familia, también es solución, en este caso una solución singular, de la ecuación de Clairaut. Ésta fue una de las primeras ocasiones en la historia en que este tipo de solución (la solución singular) se puso de relieve.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Conceptos previos

 

 

En este trabajo nos moveremos entre términos tales como “ecuación diferencial” o  “solución singular”, por lo que es conveniente realizar una definición previa de los mismos.

 

v     Ecuación diferencial. Una ecuación diferencial es una ecuación en que involucra una función incógnita desconocida junto con sus derivadas. Según el tipo de derivadas se dividen en:

·        Ecuaciones diferenciales ordinarias: La incógnita es una función de una variable y = f(x).

·        Ecuaciones en derivadas parciales: Aquellas que contienen derivadas respectos a dos o más variables

v     Orden de una ecuación diferencial. Se llama orden de la ecuación al orden de la derivada más alta que aparece en la ecuación.

v     Tipos de soluciones. Una solución de una ecuación diferencial es una función que al reemplazar a la variable dependiente, en cada caso con las derivaciones correspondientes, verifica la ecuación. Hay tres tipos de soluciones:

·        Solución General: Una solución de tipo genérico, expresada con una o más constantes. La solución general es un haz de curvas. Tiene un orden de infinitud de acuerdo a su cantidad de constantes esenciales. Una constante corresponde a una familia simplemente infinita, dos constantes a una familia doblemente infinita, etc.

·        Solución Particular: Un caso particular de la solución general, en donde la/s constante/s recibe un valor específico.

·        Solución Singular: Una función que verifica la ecuación, pero que no es un caso particular de la solución general.

 

Desarrollo

 

 

$(c, f(c)) \in D$$f: D \subset \mbox{$\ I \hspace{-1.23mm} R $\ }\rightarrow R$Supongamos que                              es una función real. Si                     , la recta tangente a la gráfica de la función en este punto está dada por:

y – f(c) = f’(c) (x – c)

 

Observemos que esta ecuación es una familia de curvas uniparamétricas con parámetro $c$. Entonces podemos encontrar una ecuación diferencial cuya solución general sea esta familia de curvas. Como y’ = f’(c), podemos reescribir la ecuación de la recta tangente como:

y = f’(c)x – cf’(c) + f(c)

Como sabemos que y’ = f’(c):

\begin{displaymath} y = xy^{\prime} + g(y^{\prime}) \end{displaymath}


La cual es la ecuación diferencial buscada. A este tipo de ecuaciones se les conoce como ecuaciones de Clairaut.

 

Teorema (Solución de la ecuación de Clairaut)

 

La ecuación de Clairaut


\begin{displaymath} y = x y^{\prime} + f(y^{\prime}) \end{displaymath}

donde f(x) es una función derivable, tiene como solución general y = cx + f(c) y como solución singular

 

\begin{displaymath} \left \{ \begin{array}{rcl} x & = & -f^{\prime}(t) \\ y & = & -t f^{\prime}(t) +f(t) \end{array} \right. \end{displaymath}

 

 

Demostración


Para resolver la ecuación hacemos la sustitución u = y’ para obtener:

 

\begin{displaymath} y = xu + f(u) \end{displaymath}

 (1)
                                   

Derivando ambos lados respecto a $x$:

\begin{displaymath} y^{\prime} = xu^{\prime} + u + f^{\prime}(u) u^{\prime} \end{displaymath}

 

de donde obtenemos que

\begin{displaymath} u^{\prime} \left( x + f^{\prime} (u) \right) = 0 \end{displaymath}

 

 

Surgen dos casos:

Caso 1:
Si u’ = 0 , entonces u = c, y sustituyendo en (1) obtenemos la solución general $y=cx + f(c)$

Caso 2:
Si x + f’(u) = 0, entonces x = -f’(u) y sustituyendo en (1), y = -uf’(u) + f(u),  es decir:  

\begin{displaymath} \left \{ \begin{array}{rcl} x & = & -f^{\prime}(u) \\ y & = & -t f^{\prime}(u) +f(u) \end{array} \right. \end{displaymath}

 

Estas son las ecuaciones paramétricas de una curva donde u es el parámetro. Obsérvese que esta solución no es un caso particular de la solución general, por lo que se trata de una solución singular.

 

 

Ejemplo

 

Resuelva la ecuación diferencial:

y = xy’ + 2 √(1 + (y’)2)

 

Solución:
La solución general es la familia de rectas y = cx ± 2 √(1 + c2 ) y como f (t)= 2 √(1 + t2 ) la solución singular está dada por:

                                                (-2) 2t                  -2t

x = - f’(t) = ―――――――― = ――――――――

                                              2 √(1 + t2 )            √(1 + t2 )

 

                                   2t2                                        -2t2 + 2 + 2t2                     

y = -tf’(t) + f(t) = ―――――――― + 2 √(1 + t2 ) = ―――――――――――― =
                                √(1 + t2 )                                       √(1 + t2 )

 

2

= ―――――――――

                                            √(1 + t2 )

 

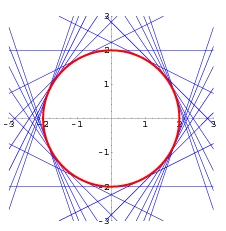
Estas son las ecuaciones paramétricas de un círculo de radio 2. En la figura siguiente se muestra la familia de rectas tangentes y la envolvente.

$x² + y^2 =4 $$y=cx \pm 2 \sqrt {1+ c^2}$            Envolvente                      y rectas tangentes

Biografía de Alexis-Claude Clairaut

 

El conocer la trayectoria vital de Clairaut nos puede ayudar a saber en qué circunstancias surgió su interés por la ecuación que lleva su nombre, para así comprenderla de un modo más exhaustivo.

 

Astrónomo y uno de los matemáticos más precoces de todos los tiempos, superando incluso a Blaise Pascal (1623-1662). Se cuenta que a la edad de diez años ya leía los libros de Guillaume François Antoine l'Hospital (1661-1704) sobre cónicas y cálculo infinitesimal. Con tan sólo doce años de edad, Clairaut presentó una memoria sobre cuatro curvas de cuarto grado a la Academia de Ciencias de Paris, la cual, y tras haberse asegurado que era el autor verdadero, se deshizo en grandes elogios.
Nació en París el 7 de mayo de 1713 y murió en la misma ciudad el 11 de mayo de 1765. Su padre, Jean-Baptiste, era maestro de matemáticas de París y miembro de la Academia de Berlín, lo que acredita su calidad como matemático.

Con sólo dieciocho años, en 1731, publicó la obra Investigaciones sobre las curvas con doble curvatura, gracias a la cual fue admitido en la Academia de Ciencias, aunque hubo de hacerse una excepción con él, ya que el reglamento exigía una edad mínima de veinte años. En la Academia se unió a los “newtonianos”, un pequeño grupo que apoyaba la filosofía natural de Newton.

          En su tratado de 1731, Alexis Clairaut desarrolló las ideas que René Descartes (1596-1650) había sugerido, casi un siglo antes, en el estudio de las curvas del espacio mediante la consideración de las proyecciones sobre dos planos coordenados. Clairaut las llamó “curvas con doble curvatura” porque la curvatura de estas curvas está determinada por las curvaturas de las dos curvas que se obtienen por proyección de la curva original en dos planos perpendiculares. Determinó así numerosas curvas del espacio mediante intersecciones de superficies variadas, dio las ecuaciones de algunas superficies y demostró que dos de estas ecuaciones son necesarias para describir una curva en el espacio. Se encuentran también en este tratado las fórmulas de la distancia para dos y tres dimensiones, ecuaciones de superficies cuádricas, y las tangentes de curvas del espacio. Clairaut demostró también que una ecuación homogénea en las variables x, y, z (todos los términos del mismo grado) representa un cono cuyo vértice está situado en el origen.

          Clairaut publicó varios e importantes trabajos durante la década 1733-1743. En 1733 publicó Sur quelques questions de maximis et minimis, un trabajo sobre cálculo de variaciones escrito en el estilo de Johann Bernoulli  y el mismo año publicó sobre las geodésicas de las cuádricas de rotación. Otros campos de interés fueron las ecuaciones diferenciales, las ecuaciones en derivadas parciales, la teoría de superficies, el cálculo en varias variables y las series trigonométricas. Por lo que respecta a las ecuaciones diferenciales, en 1734, Clairaut se interesó por una ecuación que actualmente lleva su nombre:

                                            y=xy'+f(y'),

cuya solución general consiste en una familia de líneas rectas. La ecuación de Clairaut posee también una solución singular, siendo una de las primeras veces en la historia que este tipo de solución se pone de relieve.

          En 1735, Clairaut colaboró con la Academia de Ciencias cuando ésta se decidió a determinar “la forma de la Tierra”. Se trataba de saber si la Tierra estaba achatada por los polos, como predecía la teoría de Newton, o por el contrario estaba alargada a lo largo del eje, como afirmaban los Cassini, a partir de sus mediciones geodésicas en Francia.

          En efecto, Isaac Newton (1642-1727) había determinado de manera teórica que el radio ecuatorial de la Tierra era 1/230 más largo que el radio polar. Un método consistía en medir la longitud de arco de 1º de latitud cerca del ecuador y cerca del polo. De otra parte, Jean-Dominique Cassini (1625-1712) y su hijo Jacques Cassini (1677-1756) habían efectuado una medición en 1712 y su resultado reveló que el diámetro que unía los dos polos era 1/95 más largo que el diámetro ecuatorial, lo que contradecía el resultado teórico de Newton. La Academia de Ciencias organizó entonces dos expediciones, una a Laponia (1736-1737), bajo la dirección de Pierre Louis Moreau de Maupertuis (1698-1759), y otra a Perú (1735-1744). Clairaut acompañó a Maupertuis a Laponia y las mediciones efectuadas en las dos expediciones confirmaron que la Tierra estaba achatada en los polos. De esta forma la teoría de Newton triunfó y el debate entre newtonianos y cassinianos quedó, temporalmente, zanjado. Sin embargo, no sería hasta el siglo XX cuando se conocería la respuesta definitiva a la forma de la Tierra.

             En 1739 y 1740, Clairaut publicó más trabajos sobre el cálculo integral, en particular sobre la existencia de factores integrantes para la resolver ecuaciones diferenciales de primer orden (un tema que interesó también a Johhann Bernoulli  y Reyneau). Concretamente, en 1740 publica su obra Sobre la integración o la construcción de las ecuaciones diferenciales de primer orden, donde introduce, independientemente de Leonhard Euler (1707-1783), el uso del factor integrante.

            Un año después, en 1741, publica una de sus principales obras, Elementos de geometría, dirigida especialmente para principiantes y escrito con un estilo muy simple y didáctico. En el prólogo de dicho libro pueden encontrarse las siguientes palabras: “No es admisible comenzar el estudio de la geometría desde lo más abstracto, es decir: punto, recta, plano. Quien comienza, debe partir de lo concreto a lo abstracto. Con un comienzo abstracto el novicio se alejará para siempre de las matemáticas”.

Sus cualidades de autor-pedagogo se verían después confirmadas con su obra Elementos de álgebra (1746), que tuvo una influencia notable en la enseñanza superior francesa. Su estilo huye de las demostraciones rigurosas y busca despertar la intuición y la curiosidad del lector, de forma que sea él mismo quien vaya descubriendo y explorando este nuevo mundo. Desgraciadamente parece que, según el abate Bossut, su excesiva afición a los placeres terrenales y a la compañía de las mujeres le hizo perder el reposo y la salud, provocándole la muerte de 1765.

 

 

 

 

 

 

 

Bibliografía

*      Zill, Dennis G. Ecuaciones diferenciales con aplicaciones. Grupo Editorial Iberoamérica. 2ª Edición. 1988.

 

*      www.wikipedia.org

 

*      www.divulgamat.net

 

*      Enciclopedia Espasa